Question

【题目】如图，四边形OQRP为矩形，其中P，Q分别是函数f（x）= sinwx（A＞0，w＞0）图象上的一个最高点和最低点，O为坐标原点，R为图象与x轴的交点．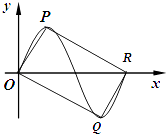

（1）求f（x）的解析式
（2）对于x∈[0，3]，方程f2（x）﹣af（x）+1=0恒有四个不同的实数根，求实数a的取值范围

Answer 1

【答案】
（1）解：由题意知，wx= ，故P（ ， ），

wx= ，故Q（ ，﹣ ），

∵ = ﹣3=0，

故w= ；

故f（x）= sin x；

（2）解：结合函数f（x）在[0，3]上的图象，

∵对于x∈[0，3]，方程f2（x）﹣af（x）+1=0恒有四个不同的实数根，

∴方程x2﹣ax+1=0在[0， ）上有两个不同的解，

∴ ，

解得，2＜a＜ ；

故实数a的取值范围为（2， ）

【解析】（1）由题意知P（ ， ），Q（ ，﹣ ），从而利用平面向量垂直求解析式；（2）由题意知方程x2﹣ax+1=0在[0， ）上有两个不同的解，从而解得．