题目内容
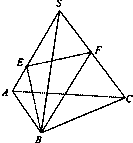
正三棱锥S-ABC中，AB=2，SB=| 3 |
分析：利用条件判断M为SQ的中点，求出 DE=1，CM=
，代入三角形CDE的面积公式进行运算．
| ||
| 2 |
解答：
解：由Q为边AB的中点得SQ⊥AB，又SQ⊥平面CDE，
可得 DE∥AB，SQ⊥CM．
设SQ交DE于M点，
另由正三棱锥S-ABC中，AB=2，SB=
，可得 CQ=
，SC=
，
∴M为SQ的中点，从而DE是SAB的中位线，求得DE=1，CM=
，
则三角形CDE的面积为
DE×CM=
，
故答案为
．
解：由Q为边AB的中点得SQ⊥AB，又SQ⊥平面CDE，可得 DE∥AB，SQ⊥CM．
设SQ交DE于M点，
另由正三棱锥S-ABC中，AB=2，SB=
| 3 |
| 3 |
| 3 |
∴M为SQ的中点，从而DE是SAB的中位线，求得DE=1，CM=
| ||
| 2 |
则三角形CDE的面积为
| 1 |
| 2 |
| ||
| 4 |
故答案为
| ||
| 4 |
点评：本题考查棱锥的结构特征，线线、线面平行垂直的判定，勾股定理求线段的长度以及求三角形的面积，属于
基础题．
基础题．
练习册系列答案
相关题目
如图，正三棱锥S-ABC中，∠BSC=40°，SB=2，一质点自点B出发，沿着三棱锥的侧面绕行一周回到点B的最短路线的长为（ ）