题目内容
 如图,△ABC是边长为
如图,△ABC是边长为 的等边三角形,P是以C为圆心,1为半径的圆上的任意一点,则
的等边三角形,P是以C为圆心,1为半径的圆上的任意一点,则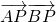 的取值范围是________.
的取值范围是________.
[1,13]
分析:根据△ABC是边长为 的等边三角形,算出
的等边三角形,算出 •
• =6,分别将
=6,分别将 和
和 分解为以
分解为以 、
、 和
和 为基向量的式子,将数量积
为基向量的式子,将数量积 •
• 展开,化简整理得
展开,化简整理得 •
• =7+
=7+ (
( +
+ ),最后研究
),最后研究 +
+ 的大小与方向,可得
的大小与方向,可得 (
( +
+ )的最大、最小值,最终得到
)的最大、最小值,最终得到 •
• 的取值范围.
的取值范围.
解答:∵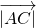 =
=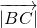 =
= ,∠ACB=60°
,∠ACB=60°
∴ •
• =
= •
• cos60°=6
cos60°=6
∵ =
= +
+ ,
, =
= +
+
∴ •
• =(
=( +
+ )(
)( +
+ )=
)= •
• +
+ (
( +
+ )+
)+ 2
2
∵ =1
=1
∴ •
• =6+
=6+ (
( +
+ )+1=7+
)+1=7+ (
( +
+ )
)
∵△ABC是边长为 的等边三角形,
的等边三角形,
∴向量 +
+ 是与AB垂直且方向向上,长度为6的一个向量
是与AB垂直且方向向上,长度为6的一个向量
由此可得,点P在圆C上运动,当 与
与 +
+ 共线同向时,
共线同向时, (
( +
+ )取最大值,且这个最大值为6
)取最大值,且这个最大值为6
当 与
与 +
+ 共线反向时,
共线反向时, (
( +
+ )取最小值,且这个最小值为-6
)取最小值,且这个最小值为-6
故 •
• 的最大值为7+6=13,最小值为7-6=1.即
的最大值为7+6=13,最小值为7-6=1.即 •
• 的取值范围是[1,13]
的取值范围是[1,13]
故答案为:[1,13]
点评:本题在等边三角形和单位圆中,求向量数量积的取值范围,着重考查了平面向量的加减法则和平面向量数量积的运算性质,属于中档题.
分析:根据△ABC是边长为
 的等边三角形,算出
的等边三角形,算出 •
• =6,分别将
=6,分别将 和
和 分解为以
分解为以 、
、 和
和 为基向量的式子,将数量积
为基向量的式子,将数量积 •
• 展开,化简整理得
展开,化简整理得 •
• =7+
=7+ (
( +
+ ),最后研究
),最后研究 +
+ 的大小与方向,可得
的大小与方向,可得 (
( +
+ )的最大、最小值,最终得到
)的最大、最小值,最终得到 •
• 的取值范围.
的取值范围.解答:∵
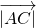 =
=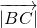 =
= ,∠ACB=60°
,∠ACB=60°∴
 •
• =
= •
• cos60°=6
cos60°=6∵
 =
= +
+ ,
, =
= +
+
∴
 •
• =(
=( +
+ )(
)( +
+ )=
)= •
• +
+ (
( +
+ )+
)+ 2
2∵
 =1
=1∴
 •
• =6+
=6+ (
( +
+ )+1=7+
)+1=7+ (
( +
+ )
)∵△ABC是边长为
 的等边三角形,
的等边三角形,∴向量
 +
+ 是与AB垂直且方向向上,长度为6的一个向量
是与AB垂直且方向向上,长度为6的一个向量由此可得,点P在圆C上运动,当
 与
与 +
+ 共线同向时,
共线同向时, (
( +
+ )取最大值,且这个最大值为6
)取最大值,且这个最大值为6当
 与
与 +
+ 共线反向时,
共线反向时, (
( +
+ )取最小值,且这个最小值为-6
)取最小值,且这个最小值为-6故
 •
• 的最大值为7+6=13,最小值为7-6=1.即
的最大值为7+6=13,最小值为7-6=1.即 •
• 的取值范围是[1,13]
的取值范围是[1,13]故答案为:[1,13]
点评:本题在等边三角形和单位圆中,求向量数量积的取值范围,着重考查了平面向量的加减法则和平面向量数量积的运算性质,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
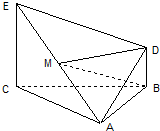 如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点. 如图,△ABC是边长为a的正三角形,现随机向圆所在区域投一点,则该点恰好落在△ABC内的概率是( )
如图,△ABC是边长为a的正三角形,现随机向圆所在区域投一点,则该点恰好落在△ABC内的概率是( ) (2012•徐州模拟)如图,△ABC是边长为
(2012•徐州模拟)如图,△ABC是边长为 (2012•江苏三模)如图,△ABC是边长为
(2012•江苏三模)如图,△ABC是边长为 (2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且
(2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且