题目内容
2.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为( )| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 可能重合 |
分析 对三点是否在平面β的同一侧进行讨论得出答案.
解答 解:若三点分布于平面β的同侧,则α与β平行,
若三点分布于平面β的两侧,则α与β相交.
故选:C.
点评 本题考查了空间平面的位置关系,属于基础题.

练习册系列答案
相关题目
13.函数y=tan $\frac{x}{2}$是( )
| A. | 周期为2π的奇函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为2π的偶函数 |
10.若弧长为4的扇形的圆心角为2rad,则该扇形的面积为( )
| A. | 4 | B. | 2 | C. | 4π | D. | 2π |
17.与两个相交平面的交线平行的直线和这两个平面的位置关系是( )
| A. | 都平行 | B. | 都相交 | ||
| C. | 在两平面内 | D. | 至少和其中一个平行 |
11.下列向量中,与(3,2)垂直的向量是( )
| A. | (3,-2) | B. | (2,3) | C. | (-3,2) | D. | (-4,6) |
12.在下列区间上函数y=sin(x+$\frac{π}{4}$)为增函数的是( )
| A. | [-$\frac{3π}{4}$,$\frac{π}{4}$] | B. | [-$\frac{π}{2}$,$\frac{π}{2}$] | C. | [-π,0] | D. | [-$\frac{π}{4}$,$\frac{3π}{4}$] |
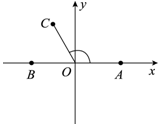 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.