题目内容
定义在(0,+∞)上的函数f(x)满足对任意m>0,n∈R有f(mn)=nf(m),且当0<x<1时f(x)<0
(1)求f(1);
(2)证明:当x>1时f(x)>0;
(3)证明:函数f(x)在(0,+∞)上递增.
(1)解:取m=1,n=2得f(12)=2f(1),
∴f(1)=0
(2)证明:设x>1,则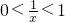 ,又0<x<1时,f(x)<0,
,又0<x<1时,f(x)<0,
∴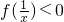
∵m>0,n∈R有f(mn)=nf(m),
∴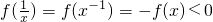
∴f(x)>0
即x>1时,f(x)>0
(3)证明:∵f(mα+β)=f(mα×mβ)=(α+β)f(m)=αf(m)+βf(m)=f(mα)+f(mβ),
记mα=x>0,mβ=y>0,则f(xy)=f(x)+f(y),
设0<x1<x2,则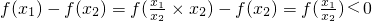 即f(x1)<f(x2),
即f(x1)<f(x2),
故函数f(x)在(0,+∞)上单增.
分析:(1)利用赋值,取m=1,n=2可求f(1)
(2)设x>1,则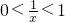 ,结合已知可得
,结合已知可得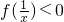 ,由f(mn)=nf(m),可得
,由f(mn)=nf(m),可得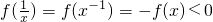 可证
可证
(3)由f(mα+β)=f(mα×mβ)=(α+β)f(m)=αf(m)+βf(m)=f(mα)+f(mβ),可得f(xy)=f(x)+f(y),设0<x1<x2,则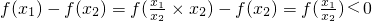 ,根据单调性的定义可证
,根据单调性的定义可证
点评:本题考查的知识点是抽象函数及其应用,赋值法是求解抽象函数的函数值的常用的方法,其中在解答抽象函数的关键是配凑
∴f(1)=0
(2)证明:设x>1,则
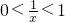 ,又0<x<1时,f(x)<0,
,又0<x<1时,f(x)<0,∴
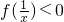
∵m>0,n∈R有f(mn)=nf(m),
∴
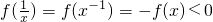
∴f(x)>0
即x>1时,f(x)>0
(3)证明:∵f(mα+β)=f(mα×mβ)=(α+β)f(m)=αf(m)+βf(m)=f(mα)+f(mβ),
记mα=x>0,mβ=y>0,则f(xy)=f(x)+f(y),
设0<x1<x2,则
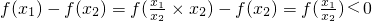 即f(x1)<f(x2),
即f(x1)<f(x2),故函数f(x)在(0,+∞)上单增.
分析:(1)利用赋值,取m=1,n=2可求f(1)
(2)设x>1,则
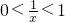 ,结合已知可得
,结合已知可得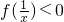 ,由f(mn)=nf(m),可得
,由f(mn)=nf(m),可得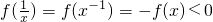 可证
可证(3)由f(mα+β)=f(mα×mβ)=(α+β)f(m)=αf(m)+βf(m)=f(mα)+f(mβ),可得f(xy)=f(x)+f(y),设0<x1<x2,则
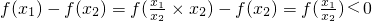 ,根据单调性的定义可证
,根据单调性的定义可证点评:本题考查的知识点是抽象函数及其应用,赋值法是求解抽象函数的函数值的常用的方法,其中在解答抽象函数的关键是配凑

练习册系列答案
相关题目
已知定义在(0,1)上的函数f(x),对任意的m,n∈(1,+∞)且m<n时,都有f(
)-f(
)=f(
)记an=f(
),n∈N*,则在数列{an}中,a1+a2+…a8=( )
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|