若x.y满足约束条件$\left\{\begin{array}{l}{y≥0}\\{x+y-4≤0}\\{x-3y≥0}\end{array}\right.$.则z=2x+y的最大值是( )A．8B．7C．4D．0 题目和参考答案——青夏教育精英家教网—

题目内容

18．若x，y满足约束条件$\left\{\begin{array}{l}{y≥0}\\{x+y-4≤0}\\{x-3y≥0}\end{array}\right.$，则z=2x+y的最大值是（　　）

A．

B．

C．

D．

分析作出可行域，由目标函数变型得y=-2x+z，根据可行域找出最优解即可．

解答解：作出约束条件$\left\{\begin{array}{l}{y≥0}\\{x+y-4≤0}\\{x-3y≥0}\end{array}\right.$表示的可行域如图所示：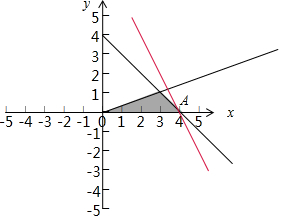

由目标函数z=2x+y得y=-2x+z，
由图象可知当直线y=-2x+z经过点A时，截距最大，即z最大．
解方程组$\left\{\begin{array}{l}{x+y=4}\\{y=0}\end{array}\right.$得x=4，y=0，即A（4，0）．
∴z的最大值为2×4+0=8．
故选：A．

点评本题考查了简单的线性规划，作出可行域寻找最优解是解题关键，属于中档题．

练习册系列答案

9．

如图，在长方形ABCD中，对角线BD与两邻边所成的角分别为α，β则cos²α+cos²β=1．仿此，在长方体ABCD-A′B′C′D′中，下列结论正确的是（　　）

	A．	若对角线BD′与面ABC，面ABB′，面BCB′所成的角为α，β，γ，则cos²α+cos²β+cos²γ=1
	B．	若对角线BD′与面ABC，面ABB′，面BCB′所成的角为α，β，γ，则cos²α+cos²β+cos²γ=2
	C．	若对角线BD′与三条棱AB，BC，BB′所成的角为α，β，γ，则cos²α+cos²β+cos²γ=2
	D．	以上类比结论均错误．

6．已知i是虚数单位，若复数-i（a+i）（a∈R）的实部与虚部相等，则a=（　　）

13．已知直线x+y-1=0和直线x-2y-4=0的交点为P．
（1）求过点P且与直线x-2y+1=0垂直的直线方程；
（2）若点Q在圆（x+1）²+y²=4上运动，求线段PQ的中点M的轨迹方程．

3．若正数 x，y，z 满足 x+2y+3z=1，则$\frac{1}{x+z}+\frac{8（x+z）}{y+z}$的最小值为9．

10．已知角α的顶点在原点，角的始边和x轴非负半轴重合，终边经过点P（4，-3）．
（1）求sinα，cosα的值；
（2）求$\frac{cos（π+α）cos（\frac{π}{2}+α）}{cos（-π-α）sin（\frac{9π}{2}+α）}$的值．

7．设变量x，y满足约束条件$\left\{\begin{array}{l}{x+2y≤8}\\{x≤4}\\{y≤3}\end{array}\right.$，则目标函数z=2x+3y的最大值为14．

8．已知函数f（x）=|x+1|-|x-2|，g（x）=x²-x+k．
（1）求f（x）的值域；
（2）?x₁∈[0，2]，?x₂∈[-1，1]，使f（x₁）≥g（x₂），求k的范围．

试题分类