题目内容
4.已知p:实数x满足(x-a)(x-3a)<0,其中a>0;q:实数x满足$\frac{x-3}{x-2}≤0$.(1)若a=1,且p,q均正确,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
分析 (1)利用绝对值不等式的解法、一元二次不等式的解法即可化简命题p,q,命题p与q都为真命题,即可得出.
(2)求出¬p是¬q的充分不必要条件得到q是p的充分不必要条件,即可解出.
解答 解:(1)当a=1,(x-1)(x-3)<0,解得1<x<3,
由$\frac{x-3}{x-2}≤0$解得2<x≤3,
∵p,q均正确,
∴2<x<3,
故实数x的取值范围为(2,3),
(2)∵¬p是¬q的充分不必要条件,
∴q是p的充分不必要条件,
∵p为a<x<3a,
∴$\left\{\begin{array}{l}{a≤2}\\{3a>3}\end{array}\right.$,
解得1<a≤2,
故实数a的取值范围(1,2].
点评 本题考查了绝对值不等式与一元二次不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 8 |
12.已知数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n}(0≤{a}_{n}<\frac{1}{2})}\\{2{a}_{n}-1(\frac{1}{2}≤{a}_{n}<1)}\end{array}\right.$,若a1=$\frac{6}{7}$,则a2011的值为( )
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
16.若复数z=$\frac{2}{1+i}$+(1-i)2,则|z|等于( )
| A. | $\sqrt{10}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
13.执行如图所示程序框图,若输出的S值为-52,则条件框内应填写( )


| A. | i<4? | B. | i<6? | C. | i<5? | D. | i>5? |
14.已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=1,$\overrightarrow{OP}$=t$\overrightarrow{OA}$,$\overrightarrow{OQ}$=(1-t)$\overrightarrow{OB}$,|$\overrightarrow{PQ}$|在t0时取最小值,当0<t0<$\frac{1}{4}$时,cosθ的取值范围为( )
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($\frac{1}{4}$,1) | D. | (-$\frac{1}{2}$,$\frac{1}{4}$) |
 如图所示函数图象,
如图所示函数图象,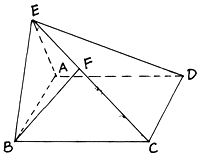 如图,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,点F在CE上,且BF⊥平面ACE;
如图,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,点F在CE上,且BF⊥平面ACE;