题目内容
(09安徽)设数列
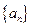 满足
满足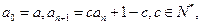 其中
其中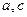 为实数,且
为实数,且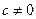
(Ⅰ)求数列
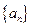 的通项公式
的通项公式(Ⅱ)设
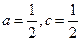 ,
,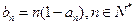 ,求数列
,求数列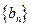 的前
的前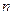 项和
项和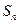 ;
;(Ⅲ)若
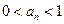 对任意
对任意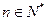 成立,证明
成立,证明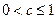
 ,
,
19解 (1) 方法一:

 当
当 时,
时, 是首项为
是首项为 ,公比为
,公比为 的等比数列。
的等比数列。
 ,即
,即  。当
。当 时,
时, 仍满足上式。
仍满足上式。
 数列
数列 的通项公式为
的通项公式为 
 。
。
方法二
由题设得:当 时,
时,


 时,
时, 也满足上式。
也满足上式。
 数列
数列 的通项公式为
的通项公式为 
 。
。
(2) 由(1)得





(3)由(1)知
若 ,则
,则


由 对任意
对任意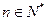 成立,知
成立,知 。下面证
。下面证 ,用反证法
,用反证法
方法一:假设 ,由函数
,由函数 的函数图象知,当
的函数图象知,当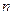 趋于无穷大时,
趋于无穷大时, 趋于无穷大
趋于无穷大
 不能对
不能对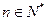 恒成立,导致矛盾。
恒成立,导致矛盾。 。
。

方法二:假设 ,
, ,
,
即 恒成立 (*)
恒成立 (*)
 为常数,
为常数, (*)式对
(*)式对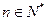 不能恒成立,导致矛盾,
不能恒成立,导致矛盾,


 当
当 时,
时, 是首项为
是首项为 ,公比为
,公比为 的等比数列。
的等比数列。 ,即
,即  。当
。当 时,
时, 仍满足上式。
仍满足上式。 数列
数列 的通项公式为
的通项公式为 
 。
。方法二
由题设得:当
 时,
时,

 时,
时, 也满足上式。
也满足上式。 数列
数列 的通项公式为
的通项公式为 
 。
。(2) 由(1)得






(3)由(1)知

若
 ,则
,则


由
 对任意
对任意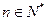 成立,知
成立,知 。下面证
。下面证 ,用反证法
,用反证法方法一:假设
 ,由函数
,由函数 的函数图象知,当
的函数图象知,当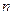 趋于无穷大时,
趋于无穷大时, 趋于无穷大
趋于无穷大 不能对
不能对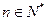 恒成立,导致矛盾。
恒成立,导致矛盾。 。
。
方法二:假设
 ,
, ,
,
即
 恒成立 (*)
恒成立 (*) 为常数,
为常数, (*)式对
(*)式对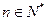 不能恒成立,导致矛盾,
不能恒成立,导致矛盾,


练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
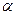 为锐角,且
为锐角,且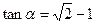 ,
,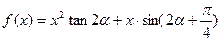 ,数列
,数列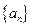 的首项
的首项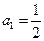 ,
,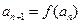 .
.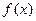 的表达式; (2)求证:
的表达式; (2)求证: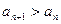 ;
;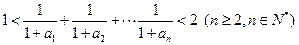 .
.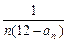 (n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn>
(n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn>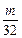 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.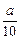 )x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
)x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形. 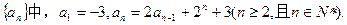
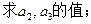 (2)设
(2)设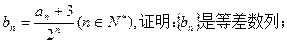
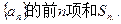

 为等差数列
为等差数列 的前
的前 项和,
项和, .
. 是等差数列.
是等差数列. 为数列
为数列 的前
的前 项和,
项和, ,
,
 的值;
的值; 是等差数列.
是等差数列.