题目内容
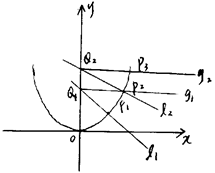
已知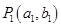 是曲线C:
是曲线C: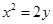 上的一点(其中
上的一点(其中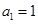 ),过点
),过点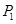 作与曲线C在
作与曲线C在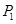 处的切线垂直的直线
处的切线垂直的直线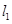 交
交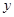 轴于点
轴于点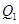 ,过
,过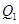 作与
作与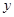 轴垂直的直线
轴垂直的直线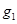 与曲线C在第一象限交于点
与曲线C在第一象限交于点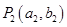 ;再过点
;再过点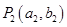 作与曲线C在
作与曲线C在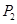 处的切线垂直的直线
处的切线垂直的直线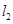 交轴于点
交轴于点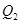 ,过
,过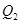 作与
作与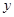 轴垂直的直线
轴垂直的直线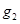 与曲线C在第一象限交于点
与曲线C在第一象限交于点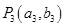 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点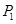 、
、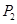 、、
、、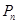 、。(其中
、。(其中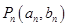 )
)
(1)求数列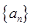 的通项公式。
的通项公式。
(2)若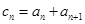 ,且
,且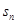 是数列
是数列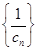 的前
的前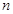 项和,
项和,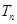 是数列
是数列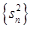 的前
的前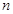 项
项
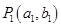 是曲线C:
是曲线C: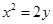 上的一点(其中
上的一点(其中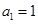 ),过点
),过点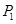 作与曲线C在
作与曲线C在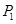 处的切线垂直的直线
处的切线垂直的直线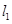 交
交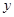 轴于点
轴于点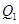 ,过
,过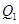 作与
作与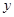 轴垂直的直线
轴垂直的直线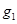 与曲线C在第一象限交于点
与曲线C在第一象限交于点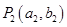 ;再过点
;再过点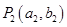 作与曲线C在
作与曲线C在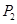 处的切线垂直的直线
处的切线垂直的直线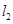 交轴于点
交轴于点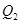 ,过
,过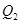 作与
作与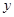 轴垂直的直线
轴垂直的直线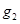 与曲线C在第一象限交于点
与曲线C在第一象限交于点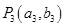 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点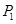 、
、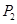 、、
、、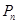 、。(其中
、。(其中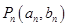 )
)
(1)求数列
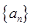 的通项公式。
的通项公式。(2)若
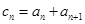 ,且
,且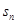 是数列
是数列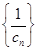 的前
的前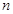 项和,
项和,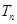 是数列
是数列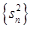 的前
的前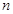 项
项(1) .(2)详见解析.
.(2)详见解析.
 .(2)详见解析.
.(2)详见解析.试题分析:(1)根据条件先找出数列中相邻项间的关系,即递推公式,然后利用递推公式求通项公式.
(2)由(1)可得
 ,由此可求出
,由此可求出 ,
,这个数列的和就不可能求出来了,怎么办?一般地,不能求和,就先放缩.
 ,将此不等式平方再相加,右边就属于等差数列的和,用公式即可求出它的和.
,将此不等式平方再相加,右边就属于等差数列的和,用公式即可求出它的和.试题解析:(1)由
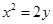 得
得 ,求导有
,求导有 1分
1分所以
 :
: ,
,令
 ,得
,得 ,所以
,所以 ,
,即
 4分
4分又
 ,得
,得 ,即
,即 6分
6分(2)∵
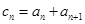
∴
 7分
7分得

=

=
 8分
8分=

<
 10分
10分∴
 11分
11分∴
 12分
12分
练习册系列答案
相关题目
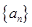 满足:
满足: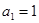 ,
,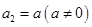 ,
,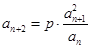 (其中
(其中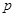 为非零常数,
为非零常数,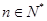 ).
).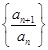 是不是等比数列?
是不是等比数列?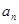 ;
;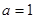 时,令
时,令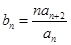 ,
,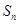 为数列
为数列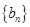 的前
的前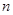 项和,求
项和,求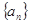 中,
中,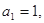 且点
且点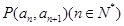 在直线
在直线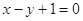 上。
上。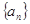 的通项公式;
的通项公式;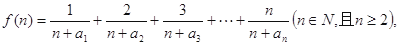 求函数
求函数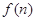 的最小值;
的最小值;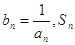 表示数列
表示数列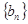 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于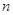 的整式
的整式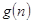 ,使得
,使得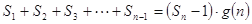 对于一切不小于2的自然数
对于一切不小于2的自然数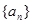 的前
的前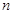 项的和为
项的和为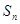 ,
, 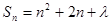 ,求证:数列
,求证:数列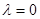 .
. 满足
满足 ,
, ,则
,则 ="_______" .
="_______" .
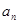 }的公差不为零,首项
}的公差不为零,首项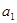 =1,
=1,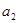 是
是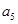 的等比中项,则数列的前10项之和是( )
的等比中项,则数列的前10项之和是( ) ,规定
,规定 为数列
为数列 .对自然数
.对自然数 ,规定
,规定 为数列
为数列

 ,则
,则 ;
; ,且满足
,且满足 ,则数列
,则数列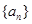 的公差为2,若
的公差为2,若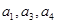 成等比数列,则a2=( )
成等比数列,则a2=( )