Question

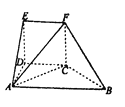
【题目】如图所示，该几何体是由一个直三棱柱和一个正四棱锥组合而成，，.

(1)证明：平面平面；

(2)求正四棱锥的高，使得该四棱锥的体积是三棱锥体积的4倍.

Answer 1

【答案】.(1) 见解析(2).

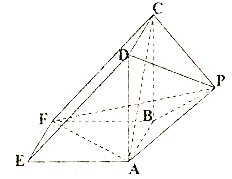
【解析】试题分析：（1）本问考查面面垂直的证明，根据面面垂直判定定理可知，需要先证明线面垂直，再证明面面垂直，根据已知直三棱柱，易知AB⊥平面ADE，则AD⊥AB，又 AD⊥AF，则易证明AD⊥平面ABEF，因此易得平面平面；（2）由于四棱锥P-ABCD为正四棱锥，根据正四棱锥的对称性可得点P到平面ABEF的距离为1，所以三棱锥P-ABF的体积为，设四棱锥的高，则，若四棱锥P-ABCD的体积是三棱锥体积的4倍，则有，则.

试题解析：(1)证明：直三棱柱中，平面，

所以：，又，

所以：平面，平面，

所以：平面平面.

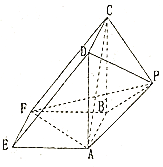
(2)到平面的距离.

所以：，

而：，所以.