题目内容
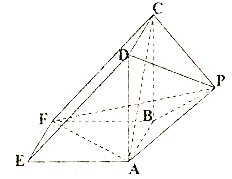
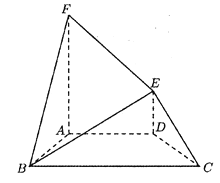
【题目】如图,几何体![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 是正方形,
是正方形, ![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 的腰长为
的腰长为![]() 的等腰直角三角形.
的等腰直角三角形.
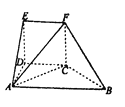
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
【答案】(I)证明过程见解析;(Ⅱ)二面角![]() 的大小为
的大小为![]() .
.
【解析】试题分析:(Ⅰ)证明![]() ,然后证明
,然后证明![]() 平面
平面![]() ,推出
,推出![]() 平面
平面![]() ,利用直线与平面垂直的性质定理证明
,利用直线与平面垂直的性质定理证明![]() ;(Ⅱ)建立空间立体直角坐标系
;(Ⅱ)建立空间立体直角坐标系![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的法向量,求出法向量之间的夹角即可求出二面角
的法向量,求出法向量之间的夹角即可求出二面角![]() 的大小.
的大小.
试题解析:
(I)证明:因为![]() 是腰长为
是腰长为![]() 的等腰直角三角形,所以
的等腰直角三角形,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
(Ⅱ)解:以点![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴建立如下图
轴建立如下图
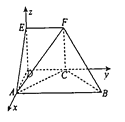
所示的空间直角坐标系:
因为![]() 是腰长为
是腰长为![]() 的等腰直角三角形,
的等腰直角三角形,
所以![]() ,
, ![]() .
.
所以![]() ,
,
![]() .
.
所以![]() .
.
则点![]() .
.
则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由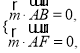 得
得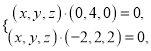 得
得![]() 得
得![]()
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量;
的一个法向量;
易知平面![]() 的一个法向量
的一个法向量![]() ;
;
设二面角![]() 的大小为
的大小为![]() ,则
,则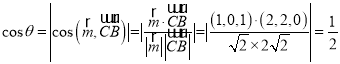 ,
,
又![]() ,解得
,解得![]() .
.
故二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
学历 | 35岁以下 | 35~50岁 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 | x | 20 | y |
(Ⅰ)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;
(Ⅱ)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为 ![]() ,求x、y的值.
,求x、y的值.