题目内容
(本 小题满分12分)
小题满分12分)
在 ABC中,
ABC中,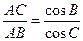 。
。
(Ⅰ)证明B=C:
(Ⅱ)若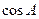 =-
=-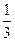 ,求sin
,求sin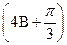 的值。
的值。
 小题满分12分)
小题满分12分)在
 ABC中,
ABC中,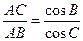 。
。(Ⅰ)证明B=C:
(Ⅱ)若
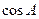 =-
=-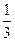 ,求sin
,求sin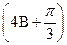 的值。
的值。(Ⅰ)见解析(Ⅱ)

本小题主要考查正弦定理、两角和与差的正弦、同角三角函数的基本关系、二倍角的正弦与余弦等基础知识,考查基本运算能力.满分12分.
(Ⅰ)证明:在△ABC中,由正弦定理及已知得 =
= .于是sinBcosC-cosBsinC=0,即sin(B-C)=0.因为
.于是sinBcosC-cosBsinC=0,即sin(B-C)=0.因为 ,从而B-C=0.
,从而B-C=0.
所以B=C.
(Ⅱ)解:由A+B+C= 和(Ⅰ)得A=
和(Ⅰ)得A= -2B,故cos2B=-cos(
-2B,故cos2B=-cos( -2B)=-cosA=
-2B)=-cosA= .
.
又0<2B< ,于是sin2B=
,于是sin2B= =
= .
.
从而sin4B=2sin2Bcos2B= ,cos4B=
,cos4B= .
.
所以
(Ⅰ)证明:在△ABC中,由正弦定理及已知得
 =
= .于是sinBcosC-cosBsinC=0,即sin(B-C)=0.因为
.于是sinBcosC-cosBsinC=0,即sin(B-C)=0.因为 ,从而B-C=0.
,从而B-C=0.所以B=C.
(Ⅱ)解:由A+B+C=
 和(Ⅰ)得A=
和(Ⅰ)得A= -2B,故cos2B=-cos(
-2B,故cos2B=-cos( -2B)=-cosA=
-2B)=-cosA= .
.又0<2B<
 ,于是sin2B=
,于是sin2B= =
= .
.从而sin4B=2sin2Bcos2B=
 ,cos4B=
,cos4B= .
.所以


练习册系列答案
相关题目
 的部分图象如图,
的部分图象如图,




 、
、 、
、 的坐标分别为
的坐标分别为 ,
, ,
, ),其中
),其中 ,
,
 ,
, 的值;
的值; ,若
,若 的最大值为
的最大值为 ,求实数
,求实数 的值.
的值. ,sin
,sin ,求角
,求角 求
求 的值.
的值.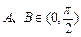 ,若
,若
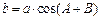 .
.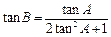 ;
;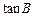 取最大值时,求
取最大值时,求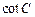 的值.
的值. 中,设
中,设 ,则
,则 的大小关系为( )
的大小关系为( )



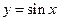 和
和 的图象在
的图象在 内的所有交点中,能确定的不同直线的条数是 ( )
内的所有交点中,能确定的不同直线的条数是 ( ) B.
B.
 D.
D.
 的图象,可由
的图象,可由 的图象经过下述哪种变换而得到 ( )
的图象经过下述哪种变换而得到 ( ) .向右平移
.向右平移 个单位,横坐标缩小到原来的
个单位,横坐标缩小到原来的 倍,纵坐标扩大到原来的
倍,纵坐标扩大到原来的 倍
倍 . 向左平移
. 向左平移 .向右平移
.向右平移 个单位,横坐标扩大到原来的
个单位,横坐标扩大到原来的 倍,纵坐标缩小到原来的
倍,纵坐标缩小到原来的 .向左平移
.向左平移