题目内容
1.若数列{an}中,a1=3,an+1=an+3,则an=( )| A. | 3 | B. | 3n+3 | C. | 3n | D. | 3n+6 |
分析 利用等差数列的通项公式即可得出.
解答 解:由an+1=an+3,∴an+1-an=3,
∴数列{an}是等差数列,公差为3.
则an=3+3(n-1)=3n.
故选:C.
点评 本题考查了等差数列的通项公式及其性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.已知全集U={1,2,3,4,5},集合A={1,3},B={3,4,5},则集合∁U(A∪B)=( )
| A. | {1,3,4,5} | B. | {3} | C. | {2} | D. | {4,5} |
10.二次函数y=x2+bx+c的图象的对称轴是x=2,则有( )
| A. | f(1)<f(2)<f(4) | B. | f(2)<f(1)<f(4) | C. | f(2)<f(4)<f(1) | D. | f(4)<f(2)<f(1) |
11.若集合A={x|x2-2x-3<0},B={x|-2<x<a},则“A∩B≠∅”的充要条件是( )
| A. | a>3 | B. | a>-1 | C. | a≥-1 | D. | a≥3 |
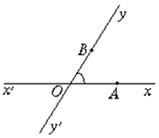 如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:
如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问: