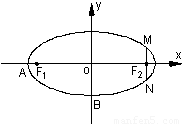
题目内容
已知
为椭圆
的左、右焦点，
是坐标原点，过
作垂直于
轴的直线
交椭圆于
.
（Ⅰ）求椭圆
的方程；
（Ⅱ）过左焦点
的直线
与椭圆交于
、
两点，若
，求直线的方程.
【答案】
(1) 
(2) 即
或
【解析】本试题主要是考查了椭圆的方程以及直线与椭圆的位置关系的运用。
解：(Ⅰ)由条件知
，且
，由
，
解得，
，
……………………………4分
所以椭圆方程为.
………………………… 5分
（Ⅱ）设点A
，B
，
当
轴时，A
，B
，所以
, ………6分
设直线
的方程为
，
代入椭圆方程得
．
……………8分
所以
……………………… 9分
由
，得
.
…………………… 10分
.
代入得
，
解得
.
…………………… 12分
所以直线的方程为
.
即或 .
练习册系列答案
相关题目
如图，在直角坐标系xOy中，已知椭圆C：
中，已知椭圆
的离心率e＝
，左右两个焦分别为
．过右焦点
且与
轴垂直的
相交M、N两点，且|MN|=1．
，
）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆
中，已知椭圆
的离心率e＝
，左右两个焦分别为
．过右焦点
且与
轴垂直的
相交M、N两点，且|MN|=1．
，
）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆
的方程为 
，双曲线
的左、右焦
与双曲线C2恒有两个不同的交点A和B，求
的范围。
+
=1（a＞b＞0）的离心率e=
，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的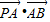
=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．