题目内容
求抛物线y2=x与直线x-y-2=0所围成的图形的面积．
分析：联解可得抛物线y2=x与直线x-y-2=0交于B（1，-1）和A（4，2），得所围成的图形面积为S=
2
dx+
(
-x+2)dx，再利用积分计算公式和运算法则，即可算出所求面积．
| ∫ | 1 0 |
| x |
| ∫ | 4 1 |
| x |
解答：
解：抛物线y2=x与直线x-y-2=0方程联解，
得两个图象交于点B（1，-1）和A（4，2），
得所围成的图形面积为：
S=
2
dx+
(
-x+2)dx=
．
故抛物线y2=x与直线x-y-2=0所围成的图形的面积是
．
解：抛物线y2=x与直线x-y-2=0方程联解，得两个图象交于点B（1，-1）和A（4，2），
得所围成的图形面积为：
S=
| ∫ | 1 0 |
| x |
| ∫ | 4 1 |
| x |
| 9 |
| 2 |
故抛物线y2=x与直线x-y-2=0所围成的图形的面积是
| 9 |
| 2 |
点评：本题给出抛物线与直线，求它们围成的图形的面积，着重考查了积分计算公式和运算法则、定积分的几何意义等知识，属于中档题．
练习册系列答案
相关题目
=
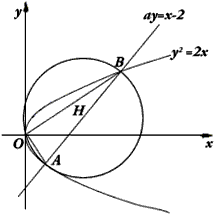
，求△BDK的内切圆M的方程。