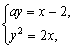题目内容
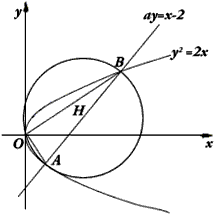
设直线ay=x-2与抛物线y2=2x交于相异两点A、B，以线段AB为直经作圆H（H为圆心），试证抛物线顶点在圆H的圆周上；并求a的值，使圆H的面积最小。
解：设
，则其坐标满足
，
消去x得
，则
，
，
因此
，即OA⊥OB，
故O必在圆H的圆周上，
又由题意圆心H
是AB的中点，
故
，
由前已证，OH应是圆H的半径，且
，
从而当a=0时，圆H的半径最小，亦使圆H的面积最小。
，则其坐标满足， 消去x得
，则，，因此
，即OA⊥OB，故O必在圆H的圆周上，
又由题意圆心H
是AB的中点，故
，由前已证，OH应是圆H的半径，且
，从而当a=0时，圆H的半径最小，亦使圆H的面积最小。
练习册系列答案
相关题目
