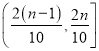题目内容
【题目】
已知
＝(cosx＋sinx，sinx)，
＝(cosx－sinx，2cosx)，
（Ⅰ）求证：向量与向量不可能平行；（Ⅱ）若f(x)＝
·，且x∈
时，求函数f(x)的最大值及最小值
【答案】（Ⅰ）见解析（2）x＝
时，f(x)有最大值
； x＝－
时，f(x)有最小值－1．
【解析】
解：（Ⅰ）假设
∥
，则2cosx(cosx＋sinx)－sinx(cosx－sinx)＝0，
∴2cos2x＋sinxcosx＋sin2x＝0，3＋sin2x＋cos2x＝0，即sin2x＋cos2x＝－3，
∴sin(2x＋)＝－
，与|sin(2x＋)|≤1矛盾，故向量与向量不可能平行．
（Ⅱ）∵f(x)＝
＝(cosx＋sinx)·(cosx－sinx)＋sinx·2cosx＝cos2x－sin2x＋2sinxcosx＝cos2x＋sin2x＝ sin(2x＋)，
∵－≤x≤，∴－≤2x＋≤
，∴当2x＋＝
，即x＝时，f(x)有最大值；
当2x＋＝－，即x＝－时，f(x)有最小值－1．
练习册系列答案
小学课时特训系列答案
相关题目
