题目内容
若x>0、y>0,则x+y>1是x2+y2>1的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.非充分非必要条件 |
先看充分性
可取x=y=
,使x+y>1成立,而x2+y2>1不能成立,故充分性不能成立;
若x2+y2>1,因为x>0、y>0,所以(x+y)2=x2+y2+2xy>x2+y2>1
∴x+y>1成立,故必要性成立
综上所述,x+y>1是x2+y2>1的必要非充分条件
故选:B
可取x=y=
| 2 |
| 3 |
若x2+y2>1,因为x>0、y>0,所以(x+y)2=x2+y2+2xy>x2+y2>1
∴x+y>1成立,故必要性成立
综上所述,x+y>1是x2+y2>1的必要非充分条件
故选:B

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 ”的否定是“
”的否定是“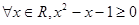 ”
” 满足x1<1<x2”和“函数
满足x1<1<x2”和“函数 在[1,2]上单调递增”同时为真
在[1,2]上单调递增”同时为真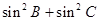 <sin2A是△ABC为钝角三角形的充要条件
<sin2A是△ABC为钝角三角形的充要条件 ”的否定是“
”的否定是“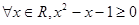 ”
” 满足x1<1<x2”和“函数
满足x1<1<x2”和“函数 在[1,2]上单调递增”同时为真
在[1,2]上单调递增”同时为真 <sin2A是△ABC为钝角三角形的充要条件.
<sin2A是△ABC为钝角三角形的充要条件.