题目内容

5．已知sinα=3cosα，那么tan2α的值为（　　）
A．2B．-2C．$\frac{3}{4}$D．-$\frac{3}{4}$

分析 利用同角三角函数基本关系式、倍角公式即可得出．

解答 解：∵sinα=3cosα，
∴tanα=3．
那么tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×3}{1-{3}^{2}}$=-$\frac{3}{4}$．
故选：C．

点评 本题考查了同角三角函数基本关系式、倍角公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
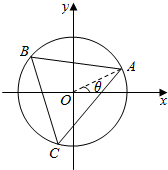15．已知Sn为数列{an}的前n项和，若an（2+sin$\frac{nπ}{2}$）=n（2+cosnπ），且S4n=an2+bn，则a-b=5．
16．已知tan（α+β）=2tanα（α，α+β≠kπ+$\frac{π}{2}$，k∈Z），求证：3sinβ=sin（2α+β）
13．如图，正三角形ABC内接于单位圆O，设∠AOx=θ，A（xA，yA），B（xB，yB），C（xC．yC）．
（1）若θ终边在第一象限，sinθ=$\frac{1}{3}$，求点C的坐标；
（2）对任意角θ，yA2+yB2+yC2是否为定值？若是，求出定值；若不是，说明理由．
20．在棱长为1的正四面体内任取一点，则该点落在正四面体内切球内的概率为$\frac{3π}{18}$．
10．-1290°角所在的象限为第二象限．
17．用计算器将下列各角由角度转换为弧度（精确到0.001）
（1）98°；
（2）59°32′．
5．设[x]表示不超过x的最大整数（如$[2]=2，[\frac{5}{4}]=1$）．对于给定的n（n＞1，n∈N*），定义$C_n^x=\frac{n（n-1）…（n-[x]+1）}{x（x-1）…（x-[x]+1）}$，x∈[1，+∞），若当$x∈[\frac{3}{2}，3）$时，函数$f（x）=C_n^x$的值域是（a，b]∪（c，d]（a，b，c，d∈R），则n的最小值是（　　）
A．5B．6C．7D．8
6．把十进制108转换为k进制数为213，则k=7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网