题目内容
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在A上,且AM= AB,点P在平面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1,在平面直角坐标系xAy中,动点P的轨迹方程是 .
AB,点P在平面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1,在平面直角坐标系xAy中,动点P的轨迹方程是 .

 AB,点P在平面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1,在平面直角坐标系xAy中,动点P的轨迹方程是 .
AB,点P在平面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1,在平面直角坐标系xAy中,动点P的轨迹方程是 . 

【思路分析】过P点作PQ⊥AD于Q,再过Q作QH⊥A1D1于H,连PH,利用三垂线定理可证PH⊥A1D1. 设P(x,y),
∵|PH|2 - |PH|2 = 1,∴x2 +1- [(x )2+y2]=1,化简得
)2+y2]=1,化简得 .
.
【命题分析】以空间图形为载体,考查直线与平面的位置关系以及轨迹方程的求法.
∵|PH|2 - |PH|2 = 1,∴x2 +1- [(x
 )2+y2]=1,化简得
)2+y2]=1,化简得 .
.【命题分析】以空间图形为载体,考查直线与平面的位置关系以及轨迹方程的求法.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 中,
中, 是等边三角形,
是等边三角形, 面ABC,已知
面ABC,已知 ,
, 在棱
在棱 上,且
上,且 ,则
,则 与平面
与平面 所成的角为( )
所成的角为( )




 ,使直线
,使直线
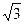 ,用
,用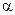 表示∠ASD,求
表示∠ASD,求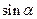
 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形 中,
中,
 ,且
,且 ,
, ,
, 分别交
分别交 于点
于点 ,将该正方形沿
,将该正方形沿 折叠,使得
折叠,使得 与
与 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱 中
中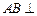
 ;
; 上有一点
上有一点 ,
, ,
, 面
面
 与平面
与平面
