题目内容
(本小题满分10分)在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 ,直线
,直线 的参数方程是
的参数方程是 (
( 为参数)。
为参数)。
(1) 求极点在直线 上的射影点
上的射影点 的极坐标;
的极坐标;
(2) 若 、
、 分别为曲线
分别为曲线 、直线
、直线 上的动点,求
上的动点,求 的最小值。
的最小值。
 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 ,直线
,直线 的参数方程是
的参数方程是 (
( 为参数)。
为参数)。(1) 求极点在直线
 上的射影点
上的射影点 的极坐标;
的极坐标;(2) 若
 、
、 分别为曲线
分别为曲线 、直线
、直线 上的动点,求
上的动点,求 的最小值。
的最小值。(1)极坐标为
(2)

(2)

解:(1)由直线的参数方程消去参数 得
得 :
: ,
,
则 的一个方向向量为
的一个方向向量为 ,
,
设 ,则
,则 ,
,
又 ,则
,则 ,得:
,得: ,
,
将 代入直线
代入直线 的参数方程得
的参数方程得 ,化为极坐标为
,化为极坐标为 。
。
(2) ,
,
由 及
及 得
得 ,
,
设 ,则
,则 到直线
到直线 的距离
的距离 ,
,
则 。
。
 得
得 :
: ,
,则
 的一个方向向量为
的一个方向向量为 ,
,设
 ,则
,则 ,
,又
 ,则
,则 ,得:
,得: ,
,将
 代入直线
代入直线 的参数方程得
的参数方程得 ,化为极坐标为
,化为极坐标为 。
。(2)
 ,
,由
 及
及 得
得 ,
,设
 ,则
,则 到直线
到直线 的距离
的距离 ,
,则
 。
。
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
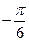 )到直线
)到直线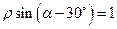 的距离是 。
的距离是 。 ,直线
,直线 垂直,则常数
垂直,则常数 = .
= .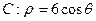 ,则圆C的半径为 。
,则圆C的半径为 。 (极点在直角坐标原点),则它的直角坐标方程为 ▲
(极点在直角坐标原点),则它的直角坐标方程为 ▲  的普通方程是 ※ .
的普通方程是 ※ .