题目内容
已知数列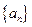 满足递推关系式:
满足递推关系式: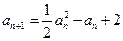 ,
,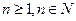 .
.
(1)若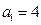 ,证明:(ⅰ)当
,证明:(ⅰ)当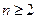 时,有
时,有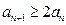 ;(ⅱ)当
;(ⅱ)当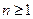 时,有
时,有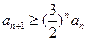 .
.
(2)若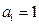 ,证明:当
,证明:当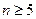 时,有
时,有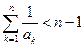 .
.
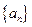 满足递推关系式:
满足递推关系式: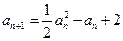 ,
,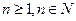 .
.(1)若
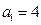 ,证明:(ⅰ)当
,证明:(ⅰ)当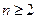 时,有
时,有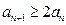 ;(ⅱ)当
;(ⅱ)当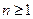 时,有
时,有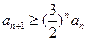 .
.(2)若
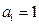 ,证明:当
,证明:当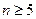 时,有
时,有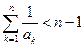 .
.证明略
因为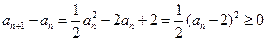 ,故
,故 ,即数列
,即数列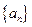 为递增数列.
为递增数列.
(1)(ⅰ)由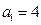 及
及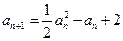 可求得
可求得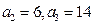 ,于是当
,于是当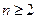 时,
时,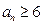 ,于是
,于是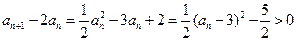 ,即当
,即当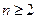 时,
时,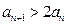 .
.
…………………………5分
(ⅱ)由于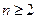 时,
时,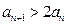 ,所以
,所以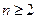 时,
时, .
.
由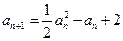 可得
可得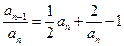 .
.
先用数学归纳法证明下面的不等式成立: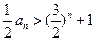 (
(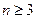 ).
).
Ⅰ)当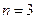 时,
时,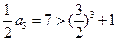 ,结论成立.
,结论成立.
Ⅱ)假设结论对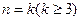 成立,即
成立,即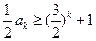 ,则结合(ⅰ)的结论可得
,则结合(ⅰ)的结论可得
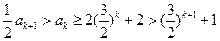 ,即当
,即当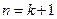 时结论也成立.
时结论也成立.
综合Ⅰ),Ⅱ)可知,不等式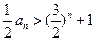 对一切
对一切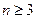 都成立.
都成立.
因此,当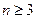 时,
时,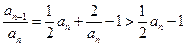
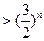 ,即
,即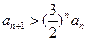 .
.
又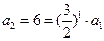 ,
,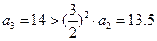 ,所以当
,所以当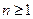 时,有
时,有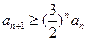 .
.
…………………………10分
(2)由于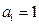 ,而数列
,而数列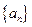 为递增数列,故当
为递增数列,故当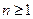 时,有
时,有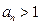 .
.
由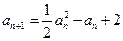 可得
可得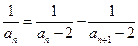 ,而
,而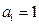 ,于是
,于是
 .
.
下面先证明:当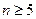 时,有
时,有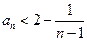 (*)
(*)
Ⅰ)根据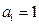 及
及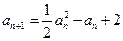 计算易得
计算易得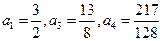 ,
,
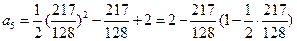 ,而
,而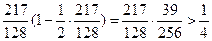 ,
,
故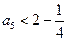 ,即当
,即当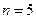 时,结论成立.
时,结论成立.
Ⅱ)假设结论对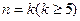 成立,即
成立,即 .
.
因为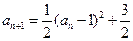 ,而函数
,而函数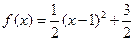 在
在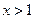 时为增函数,所以
时为增函数,所以
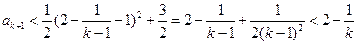 ,
,
即当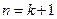 时结论也成立.
时结论也成立.
综合Ⅰ),Ⅱ)可知,不等式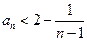 对一切
对一切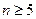 都成立.
都成立.
于是当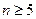 时,
时,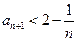 ,故
,故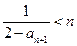 ,所以
,所以 .
.
…………………………20分
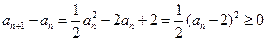 ,故
,故 ,即数列
,即数列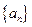 为递增数列.
为递增数列.(1)(ⅰ)由
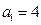 及
及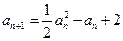 可求得
可求得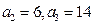 ,于是当
,于是当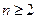 时,
时,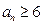 ,于是
,于是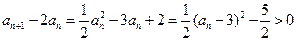 ,即当
,即当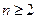 时,
时,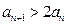 .
.…………………………5分
(ⅱ)由于
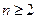 时,
时,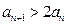 ,所以
,所以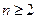 时,
时, .
.由
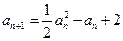 可得
可得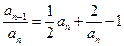 .
.先用数学归纳法证明下面的不等式成立:
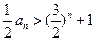 (
(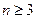 ).
).Ⅰ)当
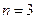 时,
时,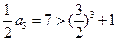 ,结论成立.
,结论成立.Ⅱ)假设结论对
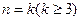 成立,即
成立,即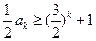 ,则结合(ⅰ)的结论可得
,则结合(ⅰ)的结论可得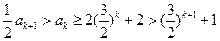 ,即当
,即当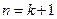 时结论也成立.
时结论也成立.综合Ⅰ),Ⅱ)可知,不等式
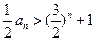 对一切
对一切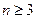 都成立.
都成立.因此,当
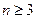 时,
时,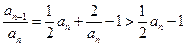
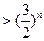 ,即
,即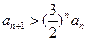 .
.又
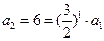 ,
,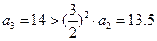 ,所以当
,所以当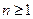 时,有
时,有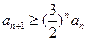 .
.…………………………10分
(2)由于
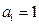 ,而数列
,而数列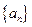 为递增数列,故当
为递增数列,故当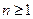 时,有
时,有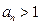 .
.由
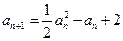 可得
可得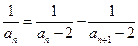 ,而
,而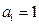 ,于是
,于是 .
.下面先证明:当
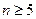 时,有
时,有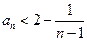 (*)
(*)Ⅰ)根据
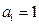 及
及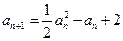 计算易得
计算易得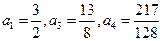 ,
,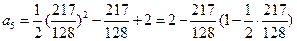 ,而
,而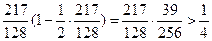 ,
,故
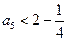 ,即当
,即当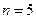 时,结论成立.
时,结论成立.Ⅱ)假设结论对
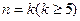 成立,即
成立,即 .
.因为
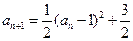 ,而函数
,而函数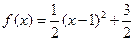 在
在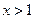 时为增函数,所以
时为增函数,所以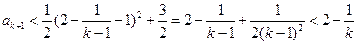 ,
,即当
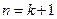 时结论也成立.
时结论也成立.综合Ⅰ),Ⅱ)可知,不等式
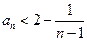 对一切
对一切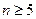 都成立.
都成立.于是当
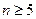 时,
时,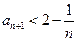 ,故
,故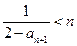 ,所以
,所以 .
.…………………………20分

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
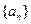 的前
的前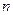 项和为
项和为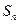 ,且
,且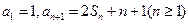 。
。 (1)求数列
(1)求数列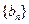 各项均为正数,满足
各项均为正数,满足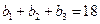 ,且
,且 ,成等比数列。证明:
,成等比数列。证明: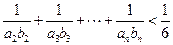 。
。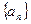 是等差数列,且
是等差数列,且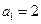 ,
,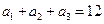 .
.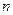 项和
项和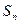 ;
;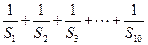 的值.
的值.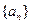 是由正数组成的比数列,
是由正数组成的比数列,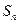 是其前
是其前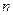 项和.
项和.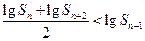 ;
;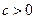 ,使得
,使得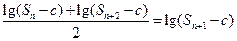 成立?并证明你的结论.
成立?并证明你的结论.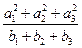 是正整数,则q等于 。
是正整数,则q等于 。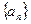 是递增数列,前n项和为
是递增数列,前n项和为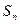 ,且
,且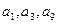 成等比数列,
成等比数列,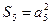 .求数列
.求数列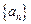 中,
中,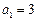 ,
,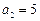 ,其前
,其前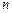 项和
项和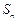 满足
满足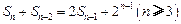 .令
.令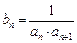 .
.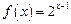 ,求证:
,求证: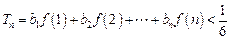 (
(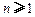 );
);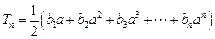 (
(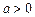 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有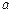 的值:①对于任意正整数
的值:①对于任意正整数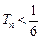 ;②对于任意的
;②对于任意的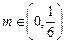 ,均存在
,均存在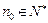 ,使得
,使得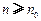 时,
时,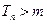 .
.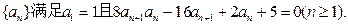 求数列
求数列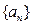 的通项公式.
的通项公式.