题目内容
已知函数f(x)＝ln x＋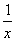
－1.
(1)求函数f(x)的单调区间；
(2)设m∈R，对任意的a∈(－1,1)，总存在x0∈[1，e]，使得不等式ma－f(x0)＜0成立，求实数m的取值范围．
解析： (1)f′(x)＝
，x＞0.
令f′(x)＞0，得x＞1，因此函数f(x)的单调递增区间是(1，＋∞)．
令f′(x)＜0，得0＜x＜1，因此函数f(x)的单调递减区间是(0,1)．
(2)依题意，ma＜f(x)max.
由(1)知，f(x)在x∈[1，e]上是增函数，
∴f(x)max＝f(e)＝ln e＋
－1＝.
∴ma＜，即ma－＜0对于任意的a∈(－1,1)恒成立．
∴
解得－≤m≤.
∴m的取值范围是
.
练习册系列答案
阅读快车系列答案
相关题目
若z的最大值为6，则z的最小值为( )
