题目内容
同时满足以下4个条件的集合记作 :(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
:(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
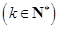 的等差数列.那么
的等差数列.那么 中元素的个数是( )
中元素的个数是( )
| A.96 | B.94 | C.92 | D.90 |
B
解析试题分析: 中元素是首项为
中元素是首项为 ,公差为
,公差为 的等差数列,那么设项数为
的等差数列,那么设项数为 ,则有
,则有 ,解得
,解得 ;
; 中元素是首项为
中元素是首项为 ,公差为
,公差为 的等差数列,那么设项数为
的等差数列,那么设项数为 ,则有
,则有 ,解得
,解得 ;
; 中元素是首项为
中元素是首项为 ,公差为
,公差为 的等差数列,那么设项数为
的等差数列,那么设项数为 ,则有
,则有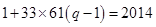 ,解得
,解得 .所以设P表示元素个数,则有:
.所以设P表示元素个数,则有: .
.
考点:1.等差数列;2.集合中元素的个数

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
设集合 ,集合
,集合 ,则集合B中元素的个数为( )
,则集合B中元素的个数为( )
| A.1 | B.2 | C.3 | D.4 |
设集合 ,
, ,则使M∩N=N成立的
,则使M∩N=N成立的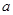 的值是( )
的值是( )
| A.1 | B.0 | C.-1 | D.1或-1 |
已知集合 ,
, ,则 ( )
,则 ( )
A. | B. | C. | D. |
在整数集 中,被5整除所得余数为
中,被5整除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,
, ,给出如下三个结论:
,给出如下三个结论:
① ;
;
② ;
;
③ ;、
;、
④“整数 、
、 属于同一“类”的充要条件是“
属于同一“类”的充要条件是“ ”.
”.
其中,正确结论的个数是( )
| A. 0 | B. 1 | C.2 | D.3 |
已知集合 ,集合
,集合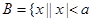 ,且
,且 ,则满足
,则满足 的实数a可以取的一个值是( )
的实数a可以取的一个值是( )
| A.0 | B.1 | C.2 | D.3 |
已知集合 则
则 ( ).
( ).
A. | B. | C.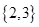 | D. |
集合A={1,2}的真子集的个数是( ).
| A.1 | B.2 | C.3 | D.4 |
 中最小的数是
中最小的数是 ;
; 不属于
不属于 属于
属于 则
则 的最小值为
的最小值为 ;
; 的解可表示为
的解可表示为 ;
; 个
个 个
个