题目内容
集合A={1,2}的真子集的个数是( ).
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:因为集合A={1,2}有2个元素,所以真子集的个数为 。
。
考点:子集;真子集。
点评:熟记公式:若集合中有n个元素,则它有 个子集,有
个子集,有 个非空子集,有
个非空子集,有 个非空真子集。
个非空真子集。

练习册系列答案
相关题目
符号“ ”可表示为
”可表示为
A. | B. |
C. | D. |
同时满足以下4个条件的集合记作 :(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
:(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
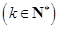 的等差数列.那么
的等差数列.那么 中元素的个数是( )
中元素的个数是( )
| A.96 | B.94 | C.92 | D.90 |
如图是《集合》的知识结构图,如果要加入“交集”,则应该放在
| A.“集合的概念”的下位 |
| B.“集合的表示”的下位 |
| C.“基本关系”的下位 |
| D.“基本运算”的下位 |
下列四个集合中,表示空集的是( )
A. | B. |
C. | D. |
已知集合
 则( )
则( )
A. | B. | C. | D. |
设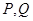 为两个非空集合,定义集合
为两个非空集合,定义集合 ,若
,若 ,
, ,则
,则 中的元素个数是
中的元素个数是
| A.9 | B.7 | C.6 | D.8 |
 ,
,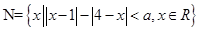
 ,则实的数
,则实的数 取值范围是____________ .
取值范围是____________ . 的方程
的方程 ,给出下列四个命题:
,给出下列四个命题: ,使得方程恰有
,使得方程恰有 个不同的实根; ②存在实数
个不同的实根; ②存在实数 个不同的实根;
个不同的实根; 个不同的实根; ④存在实数
个不同的实根; ④存在实数 个不同的实根;其中假命题的个数是( )
个不同的实根;其中假命题的个数是( ) 个
个  个
个  个
个