题目内容
设 ,则
,则 的大小关系是( )
的大小关系是( )
| A.a>c>b | B.a>b>c |
| C.c>a>b | D.b>c>a |
A
解析试题分析:因为 在
在 上是增函数,所以
上是增函数,所以 又因为
又因为 在
在 上是减函数,所以
上是减函数,所以 .
.
考点:本小题主要考查利用指数函数与幂函数的单调性比较数的大小,考查学生的推理能力和数形结合思想的应用.
点评:同底数的两个数比较大小,考虑用指数函数的单调性;同指数的两个数比较大小,考虑用幂函数的单调性,有时需要取中间量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值1叫做
的最小值1叫做 的上确界,若
的上确界,若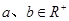 ,且
,且 ,则
,则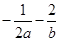 的上确界为( )
的上确界为( )
A. | B. | C. | D.-4 |
已知三个数 ,则三个数的大小关系是( )
,则三个数的大小关系是( )
A. | B. |
C. | D. |

 的零点个数为
的零点个数为
| A.3 | B.2 | C.1 | D.0 |
对实数a和b,定义运算“?”:a?b= ,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
A.(-∞,-2]∪ | B. |
C. | D.(-∞,-2]∪ |
定义在 上的函数
上的函数 ;当
;当 时,
时, ,若
,若 ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. | B. | C. | D. |
设函数 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
计算 等于 ( )
等于 ( )
A. | B. | C. | D.1 |
 的图像大致形状是( )
的图像大致形状是( )