题目内容
已知等差数列 满足:
满足: .
.
(Ⅰ)求 的通项公式及前
的通项公式及前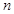 项和
项和 ;
;
(Ⅱ)若等比数列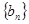 的前
的前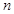 项和为
项和为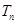 ,且
,且 ,求
,求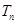 .
.
(I) ; (II)
; (II) .
.
解析试题分析:(Ⅰ)设等差数列 的公差为
的公差为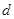 ,由
,由 得两个含首项
得两个含首项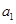 和公差
和公差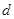 的方程,解这个方程组求得
的方程,解这个方程组求得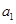 和
和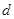 ,即可得通项公式,再利用等差数列的求和公式即可得前
,即可得通项公式,再利用等差数列的求和公式即可得前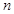 项和
项和 .
.
(Ⅱ)设等比数列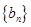 的公比为
的公比为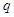 ,由(Ⅰ)和题设得:
,由(Ⅰ)和题设得: ,
,  ,再用等比数列的通项公式即可求得公比,然后用等比数列的求和公式即可求得前
,再用等比数列的通项公式即可求得公比,然后用等比数列的求和公式即可求得前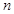 项和
项和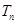 .
.
试题解析:(Ⅰ)设等差数列 的公差为
的公差为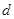 ,由题设得:
,由题设得: , (2分)
, (2分)
即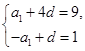 ,解得
,解得 . (4分)
. (4分) , (5分)
, (5分)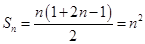 . (7分)
. (7分)
(Ⅱ)设等比数列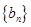 的公比为
的公比为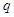 ,由(Ⅰ)和题设得:
,由(Ⅰ)和题设得: ,
,  . (9分)
. (9分)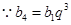 , (10分)
, (10分)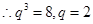 . (11分)
. (11分)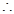 数列
数列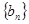 是以
是以 为首项,公比
为首项,公比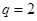 的等比数列.
的等比数列. 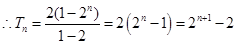 . (13分)
. (13分)
考点:等差数列与等比数列.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
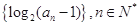 为等差数列,且
为等差数列,且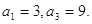
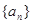 的通项公式;
的通项公式;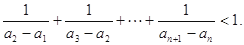
 的前6项和为60,且
的前6项和为60,且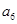 为
为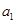 和
和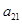 的等比中项.
的等比中项.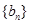 满足
满足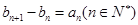 ,且
,且 ,求数列
,求数列 的前
的前 项和
项和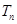 .
.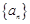 中,
中,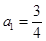 ,
,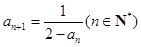 .
.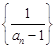 是等差数列,并求
是等差数列,并求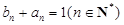 ,
,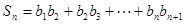 ,试比较
,试比较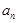 与
与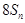 的大小.
的大小. (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;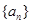 的前n项和为
的前n项和为 ,
,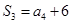 ,且
,且 成等比数列.
成等比数列.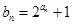 ,求数列
,求数列 的前n项和.
的前n项和.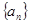 中,
中,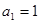 ,公差
,公差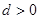 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列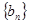 的第2项,第3项,第4项.
的第2项,第3项,第4项.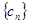 对任意自然数均有
对任意自然数均有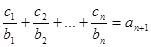 成立,求
成立,求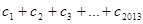 的值.
的值.