题目内容
等差数列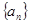 中,
中,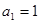 ,公差
,公差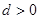 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列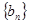 的第2项,第3项,第4项.
的第2项,第3项,第4项.
(Ⅰ)求数列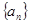 与
与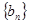 的通项公式;
的通项公式;
(Ⅱ)设数列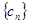 对任意自然数均有
对任意自然数均有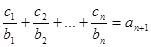 成立,求
成立,求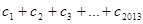 的值.
的值.
(Ⅰ) ,
, ; (Ⅱ)
; (Ⅱ)
解析试题分析:(Ⅰ) 通过等差数列的通项公式即等比中项可求得公差.即可求出等差数列的通项公式,等比数列的通项公式.
(Ⅱ)由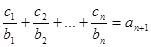 通过递推,然后求差即可
通过递推,然后求差即可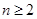 时.
时. 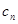 的通项公式.再结合n=1的式子.可求得
的通项公式.再结合n=1的式子.可求得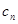 的分段形式.再对数列
的分段形式.再对数列 求前2013项的和.该数列主要是一个利用错位相减法求和的方法.本小题的关键是利用递推的思想求出
求前2013项的和.该数列主要是一个利用错位相减法求和的方法.本小题的关键是利用递推的思想求出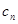 的通项.
的通项.
试题解析:(Ⅰ)由题意得:(1+d)(1+13d)= ,d>0 1分
,d>0 1分
解得:d=2 3分
所以 4分
4分 6分
6分
(Ⅱ)当n=1时,
当 ,得
,得 9分
9分 10分
10分 13分
13分
考点:1.等差数列与等比数列的通项公式.2.数列的递推思想.3.错位相减法的知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足:
满足: .
. 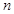 项和
项和 ;
;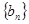 的前
的前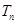 ,且
,且 ,求
,求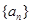 为首项为1的等差数列,其公差
为首项为1的等差数列,其公差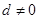 ,且
,且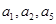 成等比数列.
成等比数列.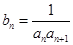 ,数列
,数列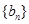 的前
的前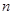 项和
项和 ,求
,求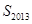 .
. 中,
中,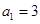 ,
, ,
,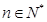 .
. 是等比数列,并求数列
是等比数列,并求数列 且
且 ,
,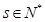 ,求证:使得
,求证:使得 ,
,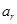 ,
, 成等差数列的点列
成等差数列的点列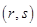 在某一直线上.
在某一直线上.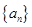 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数. ,
, ,
, ,求数列
,求数列 ,
, ,
, ,且
,且 ,求数列
,求数列 的等比数列.
的等比数列.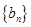 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列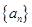 的前n项和
的前n项和 .
. , 求数列
, 求数列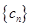 的前n项和
的前n项和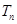 .
. 的集合:①对任意
的集合:①对任意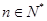 ,
,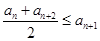 恒成立;②对任意
恒成立;②对任意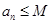 恒成立.
恒成立.
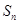 是其前n项和,且
是其前n项和,且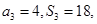 试探究数列
试探究数列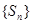 与集合W之间的关系;
与集合W之间的关系; 的通项公式为
的通项公式为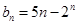 ,且
,且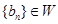 ,求M的取值范围.
,求M的取值范围. 中,
中,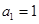 ,
, ,数列
,数列 中,
中,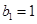 ,且点
,且点 在直线
在直线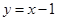 上.
上.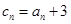 ,求数列
,求数列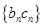 的前项和
的前项和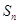 .
.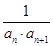 ,其前n项和为Sn.
,其前n项和为Sn.