题目内容
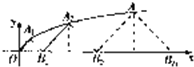 如图点An(xn,yn)是曲线y2=2x(y≥0)上的点,点Bn(an,0)是x轴上的点,△Bn-1AnBn是以An(xn,yn)为直角顶点的等腰三角形,其中n=1,2,3,…,B0为坐标原点.
如图点An(xn,yn)是曲线y2=2x(y≥0)上的点,点Bn(an,0)是x轴上的点,△Bn-1AnBn是以An(xn,yn)为直角顶点的等腰三角形,其中n=1,2,3,…,B0为坐标原点.(I)求数列{an}的通项公式;
(II)求数列bn=2n-1,求最小正整数m,使得对任意的n∈N*,当n>m时,an<bn成立.
分析:(I)由已知得抛物线方程为y=2x2,y′=2x,根据△Bn-1AnBn是等腰直角三角形得到:yn-yn-1=2,通过解直线与抛物线组成的方程组即可求出{xn},{yn}的通项公式,最后写出数列{an}的通项公式.
(II)本小题考查的知识点是数学归纳法,先猜想,当n∈N*且n>8时,an<bn成立.要证明当n>8时,an<bn,我们要先证明当n=8时,an<bn成立.再假设n=k时an<bn成立,进而证明出n=k+1时an<bn成立,即可得到对于任意当n∈N*且n>8时,an<bn成立.
(II)本小题考查的知识点是数学归纳法,先猜想,当n∈N*且n>8时,an<bn成立.要证明当n>8时,an<bn,我们要先证明当n=8时,an<bn成立.再假设n=k时an<bn成立,进而证明出n=k+1时an<bn成立,即可得到对于任意当n∈N*且n>8时,an<bn成立.
解答:解:(I)∵点An(xn,yn)在曲线y2=2x(y≥0)上,
∴An(
,yn),An-1(
,yn-1).
∵△Bn-1AnBn是等腰直角三角形,∴
-
=yn+yn-1,
∵yn+yn-1≠0,∴yn-yn-1=2.
由
可以解得x1=y1=2,
∴yn=2+2(n-1)=2n,n∈N*.
∴xn=
=2n2,∴an=xn+yn=2n(n+1),n∈N*.
(II)∵当n=8时,a8=144,b8=128,当n=9时,a9=180,b9=256,…,
可以猜想,当n∈N*且n>8时,an<bn成立.下面用数学归纳法证之.
设n=k>9时,ak<bk成立,即,2k-1>2k(k+1)成立,
当n=k+1时,bk+1=2k=2×2k-1>4k(k+1)=2(k+1)(k+2)+2(k+1)(k-2)
∵k>9,∴(k+1)(k-2)>0,∴ak+1<bk+1成立.
综上,m=8时,对任意的n∈N*,当n>m时,an<bn成立.
∴An(
| ||
| 2 |
| ||
| 2 |
∵△Bn-1AnBn是等腰直角三角形,∴
| ||
| 2 |
| ||
| 2 |
∵yn+yn-1≠0,∴yn-yn-1=2.
由
|
∴yn=2+2(n-1)=2n,n∈N*.
∴xn=
| ||
| 2 |
(II)∵当n=8时,a8=144,b8=128,当n=9时,a9=180,b9=256,…,
可以猜想,当n∈N*且n>8时,an<bn成立.下面用数学归纳法证之.
设n=k>9时,ak<bk成立,即,2k-1>2k(k+1)成立,
当n=k+1时,bk+1=2k=2×2k-1>4k(k+1)=2(k+1)(k+2)+2(k+1)(k-2)
∵k>9,∴(k+1)(k-2)>0,∴ak+1<bk+1成立.
综上,m=8时,对任意的n∈N*,当n>m时,an<bn成立.
点评:本题主要考查数列与解析几何综合的知识点,本题是一道综合性比较强的习题,解答本题的关键是准确求出数列{xn},{yn}及{an}的通项公式,熟练利用数学归纳法等知识点,此题难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图所示,A0(x0,y0)坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图所示,A0(x0,y0)坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
 ,试写出
,试写出 (不需证明);
(不需证明); 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且A(0,4),求Sn的表达式.
所表示的曲线上,并且A(0,4),求Sn的表达式.