题目内容
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).(Ⅰ)求出a1,a2,a3,并猜想an关于n的表达式(不需证明);
(Ⅱ)设bn=
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
| 1 |
| 6 |

分析:(Ⅰ)由点A1(a1,0)得到等边三角形的边长为a1根据等边三角形的性质得P1的坐标为(
,
)代入到y2=3x中求出即可得到a1,然后同理求出a2和a3,然后猜想an=n(n+1)(n∈N*);
(Ⅱ)把猜想的通项公式代入到bn中化简得到通项公式,利用bn+1-bn得到小于0,所以数列为递减数列,所以当m∈[-1,1]时,不等式t2-2mt+
>bn恒成立只需要求出bn的最大值,即可求出t的取值范围.
| a1 |
| 2 |
| ||
| 2 |
(Ⅱ)把猜想的通项公式代入到bn中化简得到通项公式,利用bn+1-bn得到小于0,所以数列为递减数列,所以当m∈[-1,1]时,不等式t2-2mt+
| 1 |
| 6 |
解答:解:(Ⅰ)由点A1(a1,0)得到第一个等边三角形的边长为a1,
根据等边三角形的性质得P1的坐标为(
,
)
代入到y2=3x中
a12=
a1,解得a1=2;
又因为点A2(a2,0),所以得第二个等边三角形的边长为a2-2,
则P2的坐标为(
,
)代入到y2=3x中解得a2=6;
因为A3(a3,0),所以第三个等边三角形的边长为a3-6,
则P3的坐标为(
,
)代入到y2=3x中解得a3=12.
所以a1=2,a2=6,a3=12;
猜想:an=n(n+1)(n∈N*).
(Ⅱ)bn=
+
+
++
=
+
++
=
-
=
=
.
bn+1-bn=
<0(n∈N*)
即bn+1<bn,所以数列{bn}是递减数列.
所以,当n=1时,(bn)max=
.
t2-2mt+
>bn(?n∈N*,?m∈[-1,1])?t2-2mt+
>(bn)max=
,
即t2-2mt>0(?m∈[-1,1])?
解之得,实数t的取值范围为(-∞,-2)∪(2,+∞).
根据等边三角形的性质得P1的坐标为(
| a1 |
| 2 |
| ||
| 2 |
代入到y2=3x中
| 3 |
| 4 |
| 3 |
| 2 |
又因为点A2(a2,0),所以得第二个等边三角形的边长为a2-2,
则P2的坐标为(
| a2-2 |
| 2 |
| ||
| 2 |
因为A3(a3,0),所以第三个等边三角形的边长为a3-6,
则P3的坐标为(
| a3-6 |
| 2 |
| ||
| 2 |
所以a1=2,a2=6,a3=12;
猜想:an=n(n+1)(n∈N*).
(Ⅱ)bn=
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
=
| 1 |
| (n+1)(n+2) |
| 1 |
| (n+2)(n+3) |
| 1 |
| 2n(2n+1) |
=
| 1 |
| n+1 |
| 1 |
| 2n+1 |
| n |
| 2n2+3n+1 |
| 1 | ||
(2n+
|
bn+1-bn=
| -(2n2+2n-1) |
| (2n2+7n+6)(2n2+3n+1) |
即bn+1<bn,所以数列{bn}是递减数列.
所以,当n=1时,(bn)max=
| 1 |
| 6 |
t2-2mt+
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
即t2-2mt>0(?m∈[-1,1])?
|
解之得,实数t的取值范围为(-∞,-2)∪(2,+∞).
点评:考查学生会根据数列的递推式判断数列是增数列还是减数列,理解函数恒成立时所取的条件,还考查学生归纳总结,作出猜想的能力.

练习册系列答案
相关题目
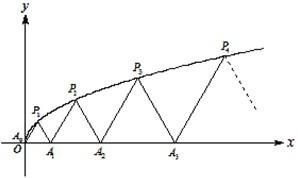 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).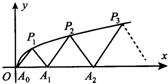 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=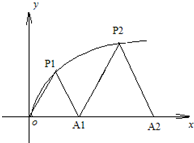 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点). (2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
(2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线