题目内容
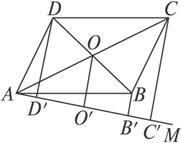
如图求证:AD′=B′C′.
图
思路分析:平行四边形对角线互相平分,容易看出O是△AC′C的边AC的中点,也是梯形BDD′B′的腰BD的中点.为此,只要过O作OO′⊥AM或OO′∥DD′易得O′分别为AC′和B′D′的中点,即O′A=O′C′,O′D′=O′B′,两式相减即得证.
证明:作OO′⊥AM,O′为垂足,
∵ABCD为平行四边形,
∴AO=CO,BO=DO.
又∵DD′,OO′,BB′,CC′都垂直于AM,
∴DD′∥OO′∥BB′∥CC′.
∴O′A=O′C′,O′D′=O′B′.
∴O′A-O′D′=O′C′-O′B′,即AD′=C′B′.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,G是△ABC的重心,过G的直线与边AB,AC相交于E,F,若
如图,G是△ABC的重心,过G的直线与边AB,AC相交于E,F,若