Question

如图1-3-5，已知在△ABC中，AB=AC，∠A=36°，BD是角平分线，试利用三角形相似的关系说明AD²=DC·AC.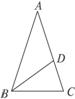

图1-3-5

Answer 1

思路分析：有一个角是36°的等腰三角形，它的底角是72°，而BD是底角的平分线，

∴∠CBD=36°，则可推出△ABC∽△BCD，进而由相似三角形的对应边成比例推出线段之间的比例关系.

证明：∵∠A=36°,AB=AC,∴∠ABC=∠C=72°.

又∵BD平分∠ABC，∴∠ABD=∠CBD=36°.

∴AD=BD=BC，且△ABC∽△BCD.∴BC∶AB=CD∶BC.

∴BC²=AB·CD.∴AD²=AC·CD.

    深化升华 (1)有两个角对应相等，那么这两个三角形相似，这是判断两个三角形相似最常用的方法，并且根据相等的角的位置，可以确定哪些边是对应边.(2)要说明线段的乘积式ab=cd或平方式a²=bc，一般都是先证明比例式或，再根据比例的基本性质推出乘积式或平方式.