题目内容
如图，互相垂直的两条公路AM、AN旁有一矩形花园ABCD，现欲将其扩建成一个更大的三角形花园APQ，要求P在射线AM上，Q在射线AN上，且PQ过点C，其中AB＝30m，AD＝20m.记三角形花园APQ的面积为S.
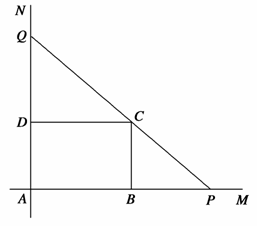
(1)当DQ的长度是多少时，S最小？并求S的最小值；
(2)要使S不小于1600m2，则DQ的长应在什么范围内？
(1)设DQ＝xm(x>0)，则AQ＝x＋20，
∵
＝
，∴
＝
，
∴AP＝
，则S＝
×AP×AQ＝
＝15(x＋
＋40)≥1200，当且仅当x＝20时取等号．
(2)∵S≥1600，∴3x2－200x＋1200≥0，∴0<x≤
或x≥60
答：(1)当DQ的长度是20m时，S最小，且S的最小值为1200m2；
(2)要使S不小于1600m2，则DQ的取值范围是0<DQ≤或DQ≥60.
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
如图，互相垂直的两条公路AM、AN旁有一矩形花园ABCD，现欲将其扩建成一个更大的三角形花园APQ，要求P在射线AM上，Q在射线AN上，且PQ过点C，其中AB=30米，AD=20米．记三角形花园APQ的面积为S．
如图，互相垂直的两条公路AP、AQ旁有一矩形花园ABCD，现欲将其扩建成一个更大的三角形花园AMN，要求点M在射线AP上，点N在射线AQ上，且直线MN过点C，其中AB=36米，AD=20米．记三角形花园AMN的面积为S．
、
旁有一矩形花园
，现欲将其扩建成一个更大的三角形花园
，要求
在射线
在射线
过点
，其中
米，
米. 记三角形花园
的长度是多少时，S最小?并求S的最小值.
平方米，则
、
旁有一矩形花园
，现欲将其扩建成一个更大的三角形花园
，要求
在射线
在射线
过点
，其中
米，
米. 记三角形花园
.
米，将
的函数.
平方米，则
如图，互相垂直的两条公路
、
旁有一矩形花园
，现欲将其扩建成一个更大的三角形花园
，要求
在射线
在射线
过点
，其中
米，
米. 记三角形花园
.
取何值时，