题目内容
如右图,在平面直角坐标系xOy中,点A在角α的终边上,且|OA|=4cosα,则当 时,点A的纵坐标y的取值范围是________.
时,点A的纵坐标y的取值范围是________.
[
分析:先由正弦的定义把纵坐标y表示出来,然后根据正弦的倍角公式把它化简为正弦型形式,最后由定义域求得其值域.
解答:因为y=|OA|sinα=4cosαsinα=2sin2α且
所以2α∈[ ,
, ],则sin2α∈[
],则sin2α∈[ ,1].
,1].
所以y∈[ ,2].
,2].
故答案为:[ ,2].
,2].
点评:三角函数问题的解决:一般需利用三角的有关公式,把原函数转化为正弦型(或余弦型)函数,再根据正弦(或余弦)函数解决.

分析:先由正弦的定义把纵坐标y表示出来,然后根据正弦的倍角公式把它化简为正弦型形式,最后由定义域求得其值域.
解答:因为y=|OA|sinα=4cosαsinα=2sin2α且

所以2α∈[
 ,
, ],则sin2α∈[
],则sin2α∈[ ,1].
,1].所以y∈[
 ,2].
,2].故答案为:[
 ,2].
,2].点评:三角函数问题的解决:一般需利用三角的有关公式,把原函数转化为正弦型(或余弦型)函数,再根据正弦(或余弦)函数解决.

练习册系列答案
相关题目
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
|
P 沿着折线A—B—C 运动时,在映射f 的作用下,动点P′的
轨迹是( )
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
C(0,1),映射f 将xOy 平面上的点P(x,y)对应到另一
个平面直角坐标系uo′v 上的点P′(2xy,x2 – y2),则当点
|
轨迹是 ( )


 中,已知“葫芦”曲线
中,已知“葫芦”曲线 由圆弧
由圆弧 与圆弧
与圆弧 相接而成,两相接点
相接而成,两相接点 均在直线
均在直线 上.圆弧
上.圆弧 ,半径为
,半径为 ;圆弧
;圆弧 .
. :
: 与“葫芦”曲线
与“葫芦”曲线 两点.当
两点.当 时,求直线
时,求直线
 中,已知“葫芦”曲线
中,已知“葫芦”曲线 由圆弧
由圆弧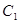 与圆弧
与圆弧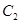 相接而成,两相接点
相接而成,两相接点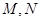 均在直线
均在直线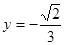 上.圆弧
上.圆弧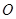 ,半径为
,半径为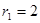 ;圆弧
;圆弧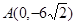 .
.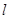 :
: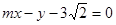 与“葫芦”曲线
与“葫芦”曲线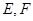 两点.当
两点.当 时,求直线
时,求直线