题目内容
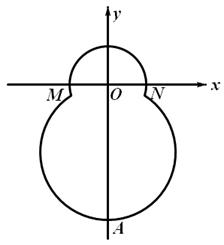
如右图,在平面直角坐标系 中,已知“葫芦”曲线
中,已知“葫芦”曲线 由圆弧
由圆弧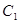 与圆弧
与圆弧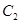 相接而成,两相接点
相接而成,两相接点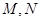 均在直线
均在直线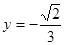 上.圆弧
上.圆弧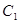 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点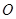 ,半径为
,半径为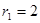 ;圆弧
;圆弧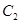 过点
过点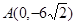 .
.
(I)求圆弧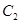 的方程;
的方程;
(II)已知直线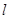 :
: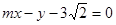 与“葫芦”曲线
与“葫芦”曲线 交于
交于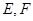 两点.当
两点.当 时,求直线
时,求直线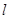 的方程.
的方程.
【答案】
解:(I)由题意,得圆弧 所在圆的方程为
所在圆的方程为 ,令
,令 ,解得
,解得 ,则线段
,则线段 的中垂线的方程为
的中垂线的方程为 ,令
,令 ,得圆弧
,得圆弧 所在圆的圆心为
所在圆的圆心为 ,又圆弧
,又圆弧 所在圆的半径为
所在圆的半径为 ,所以圆弧
,所以圆弧 的方程为
的方程为
 .……..(6分)
.……..(6分)
(II)因为 ,
, ,
, ,所以
,所以 两点分别在两个圆弧上.设点
两点分别在两个圆弧上.设点 到直线
到直线 的距离为
的距离为 ,因为直线
,因为直线 恒过圆弧
恒过圆弧 所在圆的圆心
所在圆的圆心 ,所以
,所以 ,即
,即 ,解得
,解得 ,即
,即 ,得
,得 ,所以直线
,所以直线 的方程
的方程 .
……..(12分)
.
……..(12分)
【解析】略

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
|
P 沿着折线A—B—C 运动时,在映射f 的作用下,动点P′的
轨迹是( )
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
C(0,1),映射f 将xOy 平面上的点P(x,y)对应到另一
个平面直角坐标系uo′v 上的点P′(2xy,x2 – y2),则当点
|
轨迹是 ( )
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
|
个平面直角坐标系uo′v 上的点P′(2xy,x2 – y2),则当点
P 沿着折线A—B—C 运动时,在映射f 的作用下,动点P′的
轨迹是( )


