题目内容
(本题满分12分)已知函数 的部分图象如图所示,
的部分图象如图所示, 是图象的最高点,
是图象的最高点, 为图象与
为图象与 轴的交点,
轴的交点, 为坐标原点,若
为坐标原点,若

(1)求函数 的解析式,
的解析式,
(2)将函数 的图象向右平移2个单位后得到函数
的图象向右平移2个单位后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的值域.
的值域.
(1) (2)
(2)
【解析】
试题分析:第(1)问从给出的三角函数图象中给出三个线段信息,从中可以求出图象最高点的坐标, 的长度,由此推理出三角函数的解析式;第(2)问考查三角函数图象的平移、三角函数的恒等变换及三角函数的值域等知识,求解三角函数的值域,关注自变量
的长度,由此推理出三角函数的解析式;第(2)问考查三角函数图象的平移、三角函数的恒等变换及三角函数的值域等知识,求解三角函数的值域,关注自变量 的取值范围是解题的关键,同时还要结合三角函数的图象进行分析,才能准确求出其函数值域.
的取值范围是解题的关键,同时还要结合三角函数的图象进行分析,才能准确求出其函数值域.
试题解析:(1)由条件知 ,所以
,所以 .
.
由此可得振幅 ,周期
,周期 ,又
,又 ,则
,则 .
.
将点 代入
代入 ,得
,得 ,
,
因为 ,所以
,所以 ,于是
,于是 .
.
(2)由题意可得 .
.
所以
 .
.
当 时,
时, ,所以
,所以 ,
,
即 .于是函数
.于是函数 的值域为
的值域为 .
.
考点:三角函数的图象和性质.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 ,
, ,
, (
( ),且
),且 与
与 的夹角等于
的夹角等于 的夹角,则
的夹角,则
 B.
B. C.
C. D.
D.
 是定义在R上的周期为3的函数,当
是定义在R上的周期为3的函数,当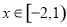 时,
时,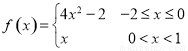 ,则
,则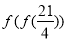 =( )
=( )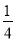 B.
B.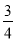 C.
C. D.0
D.0 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图象关于点(1,0)对称,若对任意的
的图象关于点(1,0)对称,若对任意的 ,
,
 ,等式
,等式 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )  .
. B.
B. C.
C. D.
D.
 }的前
}的前 项和为
项和为 ,若
,若 ,则满足
,则满足 的正整数
的正整数 .
.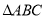 中,内角
中,内角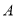 ,
,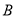 ,
,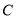 所对应的边分别为
所对应的边分别为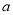 ,
, ,
,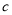 ,若
,若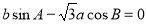 ,且
,且 ,则
,则 的值为( )
的值为( )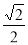 B.
B.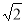 C.2 D.4
C.2 D.4 为单位向量,其中
为单位向量,其中 ,且
,且 在
在 上的投影为2,则
上的投影为2,则 与
与 的夹角
的夹角 的图象为( )
的图象为( ) B.
B. C.
C. D.
D.