题目内容
设 是定义在
是定义在 上的函数,若对任何实数
上的函数,若对任何实数 以及
以及 中的任意两数
中的任意两数 、
、 ,恒有
,恒有 ,则称
,则称 为定义在
为定义在 上的
上的 函数.
函数.
(1)证明函数 是定义域上的
是定义域上的 函数;
函数;
(2)判断函数 是否为定义域上的
是否为定义域上的 函数,请说明理由;
函数,请说明理由;
(3)若 是定义域为
是定义域为 的函数,且最小正周期为
的函数,且最小正周期为 ,试证明
,试证明 不是
不是 上的
上的 函数.
函数.
(1)证明见解析;(2)不是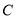 函数;(3)证明见解析.
函数;(3)证明见解析.
【解析】
试题分析:(1)利用题中所给定义进行证明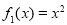 是定义域上的
是定义域上的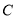 函数;(2)举反例,说明
函数;(2)举反例,说明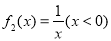 不是定义域上的
不是定义域上的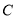 函数;(3)利用题意进行证明.
函数;(3)利用题意进行证明.
试题解析:(1)证明如下:
对任意实数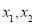 及
及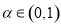 ,
,
有
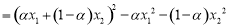 2分
2分
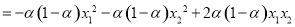
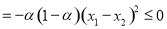 , 4分
, 4分
即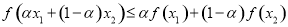 , 5分
, 5分
∴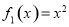 是
是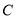 函数; 6分
函数; 6分
(2)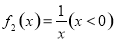 不是
不是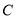 函数, 7分
函数, 7分
说明如下(举反例):
取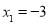 ,
,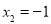 ,
,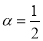 ,
,
则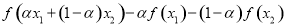
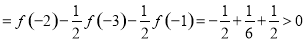 ,
,
即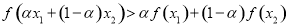 ,
,
∴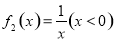 不是
不是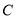 函数; 10分
函数; 10分
(3)假设 是
是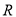 上的
上的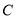 函数, 11分
函数, 11分
若存在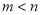 且
且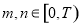 ,使得
,使得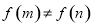 。
。
(i)若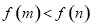 ,
,
记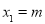 ,
,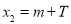 ,
,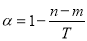 ,则
,则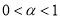 ,且
,且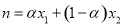 ,
,
那么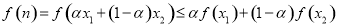
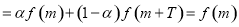 ,
,
这与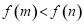 矛盾; 13分
矛盾; 13分
(ii)若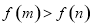 ,
,
记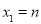 ,
,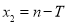 ,
,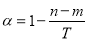 ,同理也可得到矛盾; 14分
,同理也可得到矛盾; 14分
∴ 在
在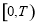 上是常数函数, 15分
上是常数函数, 15分
又因为 是周期为
是周期为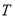 的函数,
的函数,
所以 在
在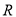 上是常数函数,这与
上是常数函数,这与 的最小正周期为
的最小正周期为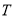 矛盾. 16分
矛盾. 16分
所以 不是
不是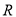 上的
上的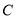 函数.
函数.
考点:1.新定义型题目;2.不等式恒成立.
考点分析: 考点1:函数的表示法 考点2:函数的周期性 考点3:函数图像的对称性 试题属性- 题型:
- 难度:
- 考核:
- 年级:

 小学课时特训系列答案
小学课时特训系列答案 的参数方程为
的参数方程为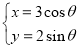 (
(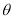 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换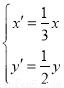 得到曲线
得到曲线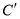 .
.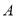 在曲线
在曲线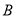
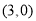 ,当点
,当点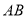 中点
中点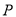 的轨迹方程.
的轨迹方程. ,且
,且 则
则 的值为( )
的值为( ) B.4 C.
B.4 C. D.
D.
 的最小值为 .
的最小值为 . 的侧棱都相等,底面
的侧棱都相等,底面 是正方形,
是正方形, 为对角线
为对角线 、
、 的交点,
的交点, ,求直线
,求直线 与面
与面 所成的角的大小.
所成的角的大小.
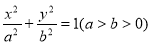 的左、右焦点分别为
的左、右焦点分别为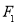 、
、 ,上顶点为
,上顶点为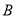 ,若
,若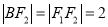 ,则该椭圆的方程为( )
,则该椭圆的方程为( )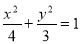 B.
B.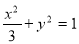 C.
C.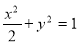 D.
D.
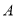 、
、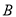 、
、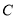 三种不同型号的产品,产品数量之比依次为
三种不同型号的产品,产品数量之比依次为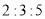 ,现用分层抽样的方法抽出一个容量为
,现用分层抽样的方法抽出一个容量为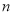 的样本,其中
的样本,其中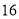 件,那么此样本的容量
件,那么此样本的容量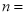 .
.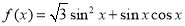 .
.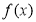 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;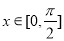 时,求函数
时,求函数 的值域.
的值域.