题目内容
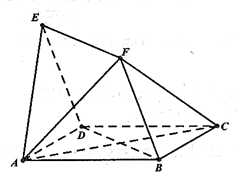
如图,四边形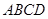 与
与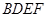 均为菱形,
均为菱形,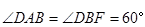 ,且
,且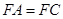 .
.
(1)求证: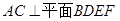 ;
;
(2)求证: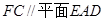 ;
;
(3)求二面角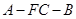 的余弦值.
的余弦值.
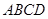 与
与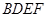 均为菱形,
均为菱形,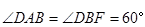 ,且
,且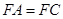 .
.
(1)求证:
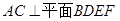 ;
;(2)求证:
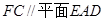 ;
;(3)求二面角
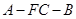 的余弦值.
的余弦值.(Ⅰ)连结FO.由四边形ABCD为菱形,得 ,且O为AC中点.
,且O为AC中点.
根据FA=FC,得到 .
.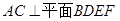 .
.
(Ⅱ)由四边形 与
与 均为菱形,
均为菱形,
得到 得出
得出
平面 ,
,  .
.
(Ⅲ)二面角A-FC-B的余弦值为 .
.
 ,且O为AC中点.
,且O为AC中点.根据FA=FC,得到
 .
.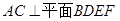 .
. (Ⅱ)由四边形
 与
与 均为菱形,
均为菱形,得到
 得出
得出
平面
 ,
,  .
.(Ⅲ)二面角A-FC-B的余弦值为
 .
. 试题分析:(Ⅰ)证明:设AC与BD相交于点O,连结FO.
因为四边形ABCD为菱形,所以
 ,且O为AC中点.
,且O为AC中点.又FA=FC,所以
 . 2分
. 2分因为
 ,
,所以
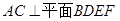 .
.  3分
3分(Ⅱ)证明:因为四边形
 与
与 均为菱形,
均为菱形,所以

因为

所以

又
 ,
,所以平面

又

所以
 . 6分
. 6分(Ⅲ)解:因为四边形BDEF为菱形,且
 ,所以
,所以 为等边三角形.
为等边三角形.因为
 为
为 中点,所以
中点,所以 由(Ⅰ)知
由(Ⅰ)知 ,故
,故 .
.由
 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系 .
.设AB=2.因为四边形ABCD为菱形,
 ,则BD=2,所以OB=1,
,则BD=2,所以OB=1, .
.所以
 . 8分
. 8分所以
 .
.设平面BFC的法向量为
 则有
则有 所以
所以
取
 ,得
,得 . 12分
. 12分易知平面
 的法向量为
的法向量为 .
.由二面角A-FC-B是锐角,得
 .
.所以二面角A-FC-B的余弦值为
 . 14分
. 14分
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离的计算。证明过程中,往往需要将立体几何问题转化成平面几何问题加以解答。本题解答,通过建立适当的空间直角坐标系,利用向量的坐标运算,简化了繁琐的证明过程,实现了“以算代证”,对计算能力要求较高。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
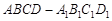 中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 . 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,点
,点 分别为
分别为 和
和 的中点.
的中点.
 ;
; 的正弦值.
的正弦值.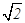 ,
,
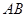 为圆
为圆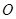 的直径,点
的直径,点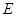 、
、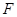 在圆
在圆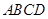 所在的平面和圆
所在的平面和圆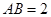 ,
,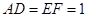 .
.
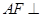 平面
平面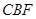 ;
;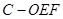 的体积.
的体积.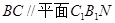 ; (2)求证:
; (2)求证: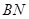
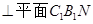 ;
; 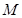 为
为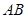 中点,在
中点,在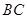 边上找一点
边上找一点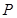 ,使
,使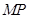
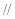 平面
平面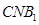 ,并求
,并求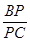 的值.
的值.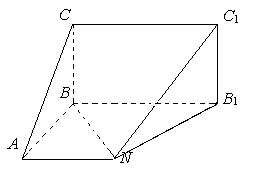
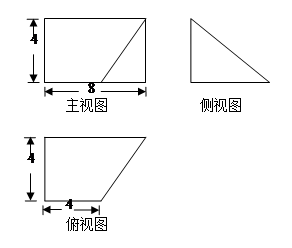
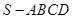 的底面边长为
的底面边长为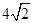 ,高
,高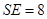 ,点
,点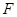 在高
在高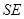 上,且
上,且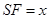 ,记过点
,记过点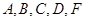 的球的半径为
的球的半径为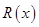 ,则函数
,则函数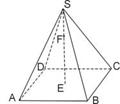
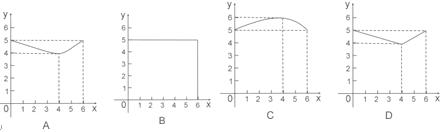
 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: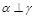 ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 ;
; ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则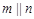 其中真命
其中真命