题目内容
设f（x）=
cos2x-
sin2x+3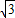
sinxcosx，则f（x）的最小正周期为（ ）A．2π
B．4π
C．π
D．
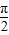
【答案】分析：函数解析式利用二倍角的正弦、余弦函数公式化简，再利用两角和与差的正弦函数公式化为一个角的正弦函数，找出ω的值，代入周期公式即可求出f（x）的最小正周期．
解答：解：f（x）=
（1+cos2x）+
（1-cos2x）+
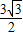sin2x=
-cos2x+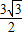
sin2x=
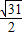sin（2x-θ）+
，（cosθ=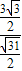
，sinθ=
），
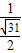∵ω=2，∴T=π．
故选C
点评：此题考查了两角和与差的正弦函数公式，二倍角的正弦、余弦函数公式，以及三角函数的周期性及其求法，熟练掌握公式是解本题的关键．
解答：解：f（x）=
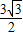（1+cos2x）+（1-cos2x）+sin2x=-cos2x+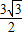sin2x=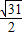sin（2x-θ）+，（cosθ=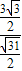，sinθ=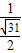），∵ω=2，∴T=π．
故选C
点评：此题考查了两角和与差的正弦函数公式，二倍角的正弦、余弦函数公式，以及三角函数的周期性及其求法，熟练掌握公式是解本题的关键．
练习册系列答案
53随堂测系列答案
相关题目
sinωxcosωx
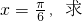ω的值．
sinωxcosωx
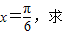ω的值．