题目内容
已知关于 的不等式
的不等式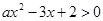 的解集为
的解集为 .
.
(1)求实数a,b的值;
(2)解关于 的不等式
的不等式 (c为常数).
(c为常数).
(1) 
(2)当 时,解集为
时,解集为 ,
,
当 时,解集为
时,解集为
当 时,解集为
时,解集为
解析试题分析:(1) 根据二次方程与二次不等式的关系可知, 且
且 是方程
是方程 的根, 则根据根与系数的关系可求出
的根, 则根据根与系数的关系可求出 值.
值.
(2)根据(1)化简分式不等式,转化为整式不等式,讨论 大小,求解集.
大小,求解集.
(1)根据二次方程与二次不等式的关系可知, 且
且 是方程
是方程 的根,
的根,
则根据根与系数的关系有 ,解得
,解得 .
.
(2)根据(1)不等式即为 ,等价于
,等价于 ,
,
当 时,解集为
时,解集为 ,
,
当 时,解集为
时,解集为
当 时,解集为
时,解集为
考点:二次方程与二次不等式的关系; 根与系数的关系;分式不等式的解法;分类讨论求解集.

练习册系列答案
相关题目
 对
对 恒成立,则实数
恒成立,则实数 的取值范围是___________.
的取值范围是___________. .
. ,求证:
,求证:
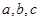 为三角形
为三角形 的三边,求证:
的三边,求证:
 .
.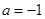 ,
, ,
, 时,求
时,求 的解集;
的解集;  ,且当
,且当 时,
时, 的最小值.
的最小值. ,
, ,若
,若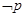 是
是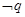 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
 .
. +
+ +
+ ≥9.
≥9.