题目内容
【题目】一位同学家里订了一份报纸，送报人每天都在早上6 : 207 : 40之间将报纸送达，该同学需要早上7 : 008 : 00之间出发上学，则这位同学在离开家之前能拿到报纸的概率为 （ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】如图所示，设送报人到达的时间为
，这位同学在离开家为
；
则
可以看成平面中的点，试验的全部结果所构成的区域为
,
其矩形区域的面积为
.
事件A所构成的区域为
.
即图中的阴影部分，其中
.
且△ABC的面积为
.
则阴影部分的面积为
.
所求对应的概率为
.
故选D.
由于随机试验落在方形区域内任何一点是等可能的，所以符合几何概型的条件。
根据题意，只要点落到阴影部分，就表示小明在离开家前能得到报纸，即事件A发生，
所以
，
故选：D.
【题目】“真人秀”热潮在我国愈演愈烈，为了了解学生是否喜欢某“真人秀”节目，在某中学随机调查了110名学生，得到如下列联表：
男 | 女 | 总计 | |
喜欢 | 40 | 20 | 60 |
不喜欢 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由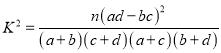
算得
.
附表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是（ ）
A. 在犯错误的概率不超过
的前提下，认为“喜欢该节目与性别有关”
B. 在犯错误的概率不超过
的前提下，认为“喜欢该节目与性别无关”
C. 有
以上的把握认为“喜欢该节目与性别有关”
D. 有
【题目】某企业生产的一种产品的广告费用
(单位:万元)与销售额
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
（1）根据上述数据，求出销售额
（万元)关于广告费用
（万元)的线性回归方程；
（2）如果企业要求该产品的销售额不少于
万元，则投入的广告费用应不少于多少万元?
（参考数值： 
.
回归直线的斜率和截距的最小二乘法估计公式分别为：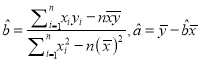 
）
