Question

（1991•云南）已知双曲线C的实半轴长与虚半轴的乘积为

3

，C的两个焦点分别为F₁，F₂，直线l过F₂且与直线F₁F₂的夹角为tanψ=

21

2

，l与线段F₁F₂的垂直平分线的交点是P，线段PF₂与双曲线C的交点为Q，且|PQ|：|QF₂|=2：1．求双曲线C的方程．

Answer 1

分析：如图，以F₁F₂所在的直线为x轴，线段F₁F₂的垂直平分线为y轴建立直角坐标系．设双曲线的方程为

x2

a2

-

y2

b2

=1(a＞0，b＞0)，可得直线PQ的方程为y=

21

2

(x-c)，得到点P的坐标．由线段的定比分点坐标公式得点Q的坐标，代入双曲线的方程即可得到

b

a

．又ab=

3

，联立即可得出．

解答：解：如图，以F₁F₂所在的直线为x轴，线段F₁F₂的垂直平分线为y轴建立直角坐标系．
设双曲线的方程为

x2

a2

-

y2

b2

=1(a＞0，b＞0)，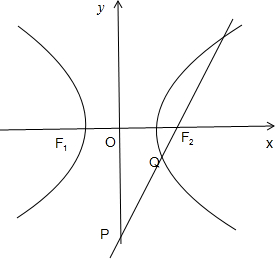
直线PQ的方程为y=

21

2

(x-c)，则P(0，-

21

2

c)，
由线段的定比分点坐标公式得xQ=

0+2c

1+2

=

2c

3

，yQ=

- 21 2 c+0

1+2

=-

21

6

c．
∴(

2c

3

，-

21

6

c)．
代入双曲线的方程得

4c2

9a2

-

21c2

36b2

=1，整理得16(

b

a

)4-41(

b

a

)2-21=0，
解得(

b

a

)2=3，或(

b

a

)2=-

7

16

．（舍去）．
∴

b

a

=

3

．又ab=

3

，
∴b=

3

，a=1．
故所求的双曲线方程为x2-

y2

3

=1．

点评：本小题考查利用坐标法研究几何问题的思想，线段的定比分点坐标公式，双曲线的有关知识及综合解题能力．