Question

若正方形ABCD边长为1，点P在对角线线段AC上运动，则

AP

 • (

PB

+

PD

)的取值范围是（　　）

• A．[0，

  1

  4

  ]
• B．[0，

  1

  9

  ]
• C．[-2，

  1

  4

  ]
• D．[-2，

  1

  9

  ]

Answer 1

分析：借助正方形的两邻边建立直角坐标系，将向量的运算转化为坐标形式的运算，利用向量的坐标形式的数量积公式表示成二次函数，通过配方找出对称轴，求出最值．

解答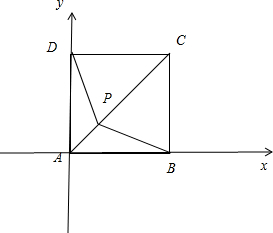：解：以AB，AC 为x，y轴建立直角坐标系则A（0，0），B（1，0），C（1，1），D（0，1）
设P（x，x）（0≤x≤1）
∵

AP

=(x，x)， 

PB

=(1-x，-x)，

PD

=(-x，1-x)
∴

AP

• (

PB

+

PD

)=2x（1-2x）=-4(x-

1

4

)2+

1

4

（0≤x≤1）
所以当x=

1

4

时，函数有最大值

1

4

；当x=1时函数有最小值-2
故答案为[-2，

1

4

]

点评：本题考查两个向量的数量积公式的应用，向量的数量积的坐标，二次函数性质的应用是解题的关键．