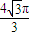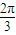题目内容
 一个棱长为a的正四面体ABCD密封容器,可充满72升溶液,后发现分别在棱AB,AC,AD上各被蚀有一小孔E,F,G,AE=
一个棱长为a的正四面体ABCD密封容器,可充满72升溶液,后发现分别在棱AB,AC,AD上各被蚀有一小孔E,F,G,AE=| a |
| 6 |
| a |
| 3 |
| a |
| 2 |
70
70
升溶液.分析:利用三角形的面积公式和锥体的体积公式,结合正四面体的性质加以计算,得出三棱锥G-AEF的体积等于正四面体ABCD体积的
.根据题意可得当E、F、G三点在同一个水平面上时,容器可盛最多的溶液.由此即可得出这容器最多可盛的溶液体积.
| 1 |
| 36 |
解答:解: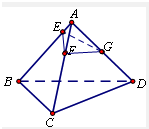 根据题意,可得当E、F、G三点在同一个水平面上时,容器可盛最多的溶液.
根据题意,可得当E、F、G三点在同一个水平面上时,容器可盛最多的溶液.
∵△AEF中,AE=
,AF=
,∠EAF=60°,
∴S△AEF=
AE•AFsin60°=
×
×
×
=
∵正四面体ABCD的棱长为a,G为AD的中点,
∴G到平面AEF的距离等于D到平面ABC距离的
,
设G到平面AEF的距离为d,则d=
×
a=
可得VG-AEF=
S△AEF×d=
×
×
=
a3
∵正四面体ABCD的体积V=
×
a2×
a=
a3
∴由正四面体ABCD密封容器可充满72升溶液,得
VG-AEF=
a3=
×
a3=
×72=2升
因此,容器最多可盛72-2=70升的溶液.
故答案为:70
 根据题意,可得当E、F、G三点在同一个水平面上时,容器可盛最多的溶液.
根据题意,可得当E、F、G三点在同一个水平面上时,容器可盛最多的溶液.∵△AEF中,AE=
| a |
| 6 |
| a |
| 3 |
∴S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 6 |
| a |
| 3 |
| ||
| 2 |
| ||
| 72 |
∵正四面体ABCD的棱长为a,G为AD的中点,
∴G到平面AEF的距离等于D到平面ABC距离的
| 1 |
| 2 |
设G到平面AEF的距离为d,则d=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
可得VG-AEF=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 72 |
| ||
| 6 |
| ||
| 432 |
∵正四面体ABCD的体积V=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| ||
| 12 |
∴由正四面体ABCD密封容器可充满72升溶液,得
VG-AEF=
| ||
| 432 |
| 1 |
| 36 |
| ||
| 12 |
| 1 |
| 36 |
因此,容器最多可盛72-2=70升的溶液.
故答案为:70
点评:本题给出实际应用问题,求容器最多可盛的溶液体积.着重考查了三角形的面积公式、锥体的体积公式和结合正四面体的性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
己知球O在一个棱长为2
的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )
| 3 |
A、4
| ||||
B、
| ||||
| C、2π | ||||
D、
|
已知球O在一个棱长为2
的正四面体内,如果球O是该正四面体的最大球,那么球O的表面积等于( )
| 3 |
A、4
| ||||
B、
| ||||
| C、2π | ||||
D、
|
 的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于
的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于

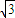 的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )
的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )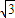 π
π