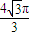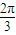题目内容
己知球O在一个棱长为2
的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )
| 3 |
A、4
| ||||
B、
| ||||
| C、2π | ||||
D、
|
分析:把球心与正四面体的四个顶点连接起来,把正四面体分成四个小三棱锥,这四个小三棱锥的体积与正四面体的体积相等,利用等体积法可求球的半径.
解答:解:设球的半径为R,正四面体的侧高为3,正四面体的高为2
,
由等体积法得:
×
×(2
)2×2
=4×
×
×(2
)2×R
∴R=
,∴球O的表面积等于4π(
)2=2π.
故选C.
| 2 |
由等体积法得:
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 2 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
∴R=
| ||
| 2 |
| ||
| 2 |
故选C.
点评:本题考查球的表面积及空间想象能力,关键在于清楚球与正四面体的位置关系,用等体积法求球的半径.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于
的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于

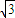 的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )
的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )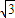 π
π