题目内容
(本小题满分12分)
已知函数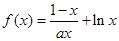
(1)若函数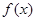 在
在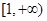 上为增函数,求正实数
上为增函数,求正实数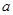 的取值范围;
的取值范围;
(2)当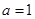 时,求
时,求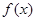 在
在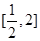 上的最大值和最小值;
上的最大值和最小值;
(3) 当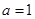 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数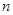 ,都有
,都有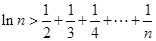 。
。
(1)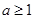 (2)最大值为
(2)最大值为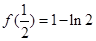 ,最小值为
,最小值为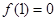 (3)
(3)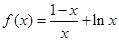 ,
,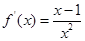
函数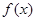 在
在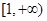 上为增函数,当
上为增函数,当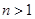 时,令
时,令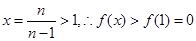
 即
即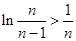 所以
所以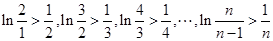
解析试题分析:(1)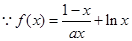 ,
,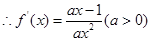
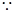 函数
函数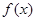 在
在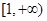 上为增函数,
上为增函数,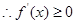 对任意的
对任意的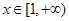 恒成立,
恒成立,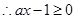 对任意的
对任意的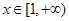 恒成立,即
恒成立,即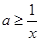 任意的
任意的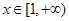 恒成立,…………2分
恒成立,…………2分
而当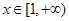 时,
时,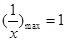 ,
,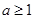 ……………………4分
……………………4分
(2)当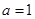 时,
时,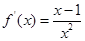
当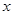 变化时,
变化时,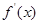 ,
,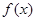 的变化情况如下表
的变化情况如下表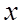
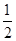
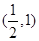
1 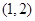
2 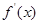
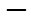
0 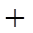
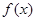
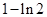
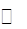
0 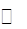
 练习册系列答案
练习册系列答案
同步导学创新成功学习系列答案
导学同步岳麓书社系列答案
一品中考系列答案
金钥匙1加1中考总复习系列答案
教与学中考全程复习导练系列答案
中考总复习优化指导系列答案
A加资源与评价系列答案
本土攻略系列答案
高分必刷系列答案
课堂活动与课后评价系列答案
相关题目
 ,求
,求 。
。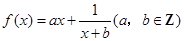 ,曲线
,曲线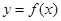 在点
在点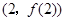 处的切线方程
处的切线方程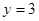 .
.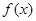 的解析式,并判断函数
的解析式,并判断函数 和直线
和直线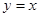 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.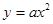 (
(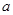 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)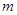 是实数,
是实数,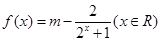 ,
, 为奇函数,求
为奇函数,求 上为单调递增函数;
上为单调递增函数;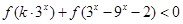 对任意
对任意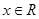 恒成立,求实数
恒成立,求实数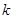 的取值范围。
的取值范围。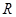 上,且满足
上,且满足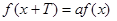 (其中常数
(其中常数 满足
满足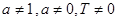 )的函数叫做似周期函数.
)的函数叫做似周期函数.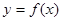 满足
满足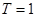 且图像关于直线
且图像关于直线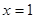 对称.求证:函数
对称.求证:函数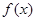 是偶函数;
是偶函数;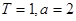 时,某个似周期函数在
时,某个似周期函数在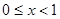 时的解析式为
时的解析式为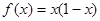 ,求函数
,求函数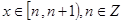 的解析式;
的解析式;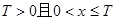 时,
时,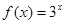 ,试研究似周期函数函数
,试研究似周期函数函数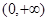 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.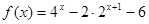 ,其中
,其中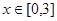 。
。 的最大值和最小值;
的最大值和最小值;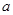 满足:
满足: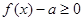 恒成立,求
恒成立,求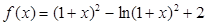 .
. 的单调增区间;
的单调增区间;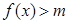 在
在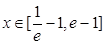 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.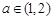 ,总存在
,总存在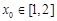 ,使不等式
,使不等式 成立,求实数m的取值范围.
成立,求实数m的取值范围.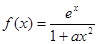 ,其中
,其中 为正实数。
为正实数。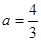 时,求
时,求 的极值点;
的极值点; 。
。 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数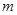 的取值范围。
的取值范围。