题目内容
(本小题12分)
已知函数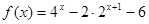 ,其中
,其中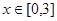 。
。
求函数 的最大值和最小值;
的最大值和最小值;
若实数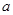 满足:
满足: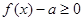 恒成立,求
恒成立,求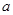 的取值范围。
的取值范围。
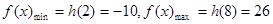 ,
,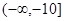
解析试题分析:解:(1)∵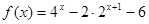
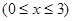
∴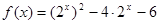
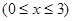 —————————————2’
—————————————2’
令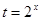 ,∵
,∵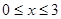 ,∴
,∴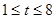 。
。
令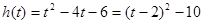 (
(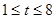 )—————————————4’
)—————————————4’
当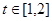 时,
时, 是减函数;当
是减函数;当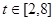 时,
时, 是增函数。
是增函数。
∴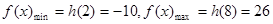 ———————————————8’
———————————————8’
(2)∵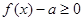 恒成立,即
恒成立,即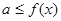 恒成立。∴
恒成立。∴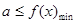 恒成立。
恒成立。
由(1)知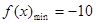 ,∴
,∴ 。
。
故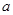 的取值范围为
的取值范围为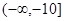 ————————————————12’
————————————————12’
考点:二次函数与不等式的恒成立问题
点评:解决该试题的关键是对于变量的整体代换求解函数的最值,同时能结合不等式恒成立分离参数来求解参数的范围属于基础题。

练习册系列答案
相关题目
 的函数
的函数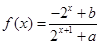 是奇函数。
是奇函数。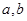 的值;
的值;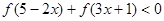
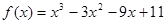
 的递减区间;
的递减区间;
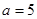 时,求函数
时,求函数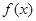 的定义域;
的定义域; 的取值范围。
的取值范围。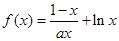
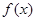 在
在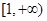 上为增函数,求正实数
上为增函数,求正实数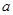 的取值范围;
的取值范围;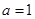 时,求
时,求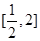 上的最大值和最小值;
上的最大值和最小值;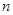 ,都有
,都有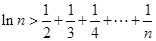 。
。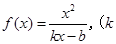 ,
,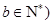 ,满足
,满足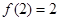 ,
,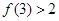 .
.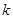 ,
,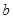 的值;
的值;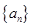 的前
的前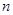 项和为
项和为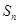 ,且有
,且有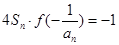 ,设
,设 ,求数列
,求数列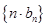 的前
的前 ;
;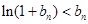 .
.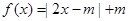 .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值;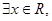 使
使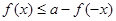 能成立,求实数a的取值范围.
能成立,求实数a的取值范围.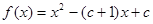
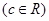 .
. 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;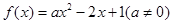 .
.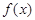 有两个零点,求
有两个零点,求 的取值范围;
的取值范围; 与
与 上各有一个零点,求
上各有一个零点,求