题目内容
【题目】已知函数![]() ,
,![]() ,且
,且![]() 在
在![]() 处取得极大值1.
处取得极大值1.
(1)求a,b的值;
(2)当![]() 时,
时,![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求出导函数![]() ,由
,由![]() 在
在![]() 处取得极大值1,可解得a,b的值;
处取得极大值1,可解得a,b的值;
(2)由![]() 得
得![]() ,整理可得
,整理可得![]() 恒成立.令
恒成立.令![]() ,则只需
,则只需![]() 的最小值大于零,分类讨论即可求出m的取值范围.
的最小值大于零,分类讨论即可求出m的取值范围.
解:(1)![]() ,
,
![]() ,
,
又![]() 在
在![]() 处取得极大值1,
处取得极大值1,
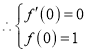 ,即
,即![]() ,解得
,解得![]() .
.
(2)由(1)知,![]() .
.
当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
等价于当![]() 时,
时,![]() 恒成立.
恒成立.
令![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,满足题意;
,满足题意;
当![]() 时,令
时,令![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递增.
上单调递增.
即![]() 在
在![]() 上单调递增,
上单调递增,
![]() .
.
(ⅰ)当![]() 时,
时,
![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
即![]() ,满足题意;
,满足题意;
(ⅱ)当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 在
在![]() 有唯一零点,设为
有唯一零点,设为![]() ,
,
![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() 当
当![]() 时,
时,![]() ,
,
![]() 不满足题意.
不满足题意.
综上,当![]() 时,
时,![]() 恒成立,
恒成立,
m的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
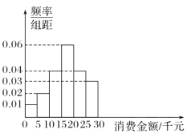
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |