题目内容
(本题13分)
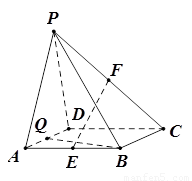
如图,在四棱锥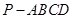 中,
中,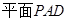
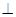 平面
平面 ,底面
,底面 是菱形,
是菱形,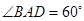 .
.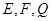 分别是
分别是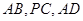 的中点.
的中点.
(1) 求证: ;
;
(2) 求证: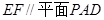 .
.
【答案】
(1)先证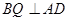 ,根据面面垂直的性质定理可知
,根据面面垂直的性质定理可知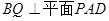
(2)先证FG//AE,且FG=AE,再证AG//EF,根据线面平行的判定定理可证.
【解析】
试题分析:(1)在菱形ABCD中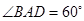 ,所以,AB=BD,
,所以,AB=BD,
因为Q是AD的中点,
所以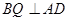 ,且
,且 ,
,
又因为,平面PAD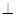 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD=AD,
平面ABCD=AD,
所以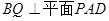 . ……6分
. ……6分
(2)取PD中点G,连接AG,FG,
因为E、F分别是AB,PC中点,
所以FG//AE,且FG=AE,
所以,四边形AEFG为平行四边形,所以,AG//EF
又因为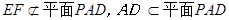
所以 。 ……13分
。 ……13分
考点:本小题主要考查线面垂直和线面平行的证明,考查学生的空间想象能力和推理能力.
点评:要证明线面垂直和线面平行,要紧扣相应的定理的条件,定理中的条件要一一列出来,缺一不可.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 关于直线
关于直线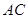 对称,
对称,
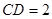 。
。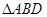 沿
沿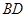 折起(如图二),使二面角
折起(如图二),使二面角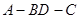 的余弦值等于
的余弦值等于 。对于图二,
。对于图二,
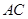 ;
;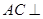 平面
平面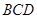 ;
;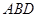 所成角的正弦值。
所成角的正弦值。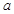 ,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积
,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积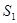 与种花的面积
与种花的面积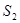 的比值
的比值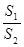 称为“草花比y”。
称为“草花比y”。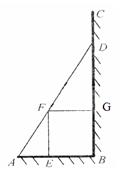
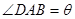 ,将
,将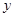 表示成
表示成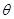 的函数关系式;
的函数关系式;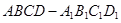 中,
中,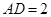 ,
,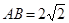 ,
,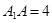 ,
, 分别是
分别是 的中点.
的中点.
 ⊥平面
⊥平面 ;
;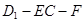 的大小.
的大小.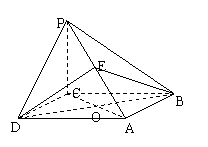 (1)求BE 与 CD所成的角.;
(1)求BE 与 CD所成的角.;