题目内容
一元二次方程mx2+(
解:∵mx2+(
∴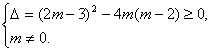
解得m≤![]() ,且m≠0.
,且m≠0.
由一元二次方程的根与系数的关系得
tanα+tanβ=![]() ,tanα·tanβ=
,tanα·tanβ=![]() ,
,
∴tan(α+β)=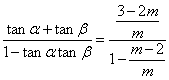 =
=![]() =
=![]() -m≥
-m≥![]() -
-![]() =-
=-![]() ,且tan(α+β)≠
,且tan(α+β)≠![]() .
.
故tan(α+β)的最小值为-![]() .
.

练习册系列答案
相关题目
题目内容
一元二次方程mx2+(
解:∵mx2+(
∴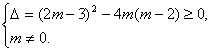
解得m≤![]() ,且m≠0.
,且m≠0.
由一元二次方程的根与系数的关系得
tanα+tanβ=![]() ,tanα·tanβ=
,tanα·tanβ=![]() ,
,
∴tan(α+β)=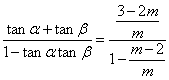 =
=![]() =
=![]() -m≥
-m≥![]() -
-![]() =-
=-![]() ,且tan(α+β)≠
,且tan(α+β)≠![]() .
.
故tan(α+β)的最小值为-![]() .
.
